Simplifique a expressão:
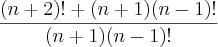
Pensei em dois meios de resolver, mas nenhum deles está de acordo com o gabarito.
Primeiro método: (Cortar o
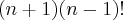 que aparece no numerador e no denominador).
que aparece no numerador e no denominador).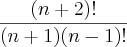
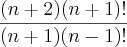
Cortando o
 que aparece no numerador e no denominador, encontro como resposta:
que aparece no numerador e no denominador, encontro como resposta: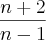
Segundo método:
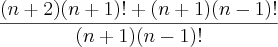
Corto o
 do numerador com o do denominador e, da mesma forma, corto também o
do numerador com o do denominador e, da mesma forma, corto também o  .
.Encontrando como resposta:

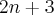
Quanto as duas resoluções, o que estou querendo saber é onde se encontra o (s) erro (s) (uma vez que a resposta não bateu com o gabarito).
Resposta do gabarito: (n+1)²
Agradeço a atenção e ajuda!



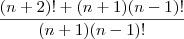
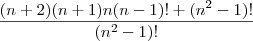
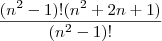



 foi desenvolvido até o
foi desenvolvido até o  (Quando postei a questão, estava usando o Ubuntu, mas creio que não seja isso.)
(Quando postei a questão, estava usando o Ubuntu, mas creio que não seja isso.)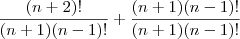
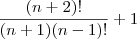
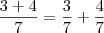
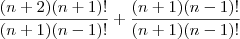
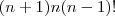 . Porque na fração do lado direito podemos simplificar? Porque é como se fosse
. Porque na fração do lado direito podemos simplificar? Porque é como se fosse  . Não corremos o risco de dividir por zero.
. Não corremos o risco de dividir por zero.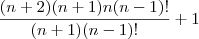
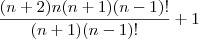
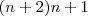
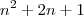


 .
.



