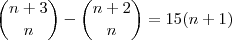
Olà eu tentei fazer este exercicio,mas gostaria de saber se é assim ?Se não for puderiam-me explicar?
A minha resolução:


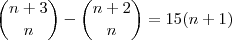


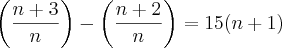
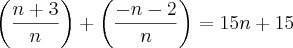
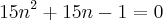




molina escreveu:Acho que o que está dentro do parênteses não é uma fração e sim uma combinação.
Achei que é isso por dois motivos:
i) não há o traço da divisão.
ii) o local onde a questão foi postada.
Abraços,

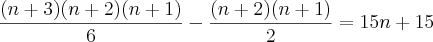


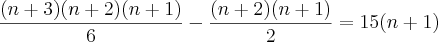
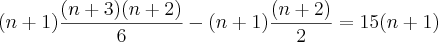
![(n+1)\left[ \frac{(n+3)(n+2)}{6}-\frac{(n+2)}{2} \right]=15(n+1) (n+1)\left[ \frac{(n+3)(n+2)}{6}-\frac{(n+2)}{2} \right]=15(n+1)](/latexrender/pictures/308154ee557eb5772c56a5c90963465e.png)
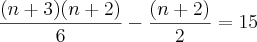
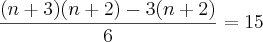
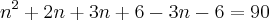
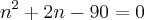



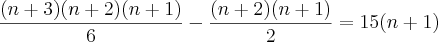
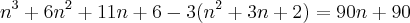
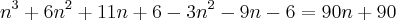
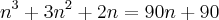

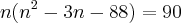



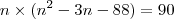
 . Veja este exemplo:
. Veja este exemplo: 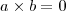 . Neste caso, você pode afirmar que um dos fatores é igual a zero pois esta é a única maneira. Agora veja este:
. Neste caso, você pode afirmar que um dos fatores é igual a zero pois esta é a única maneira. Agora veja este: 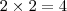 . Só porque o produto é quatro não significa que um dos seus fatores seja 4.
. Só porque o produto é quatro não significa que um dos seus fatores seja 4.


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)