 por Maou » Qua Dez 03, 2014 13:45
por Maou » Qua Dez 03, 2014 13:45
Olá tudo bom, a partir desta função y(x) = (x+1)?(1-x) derivando eu chego em y'(x) = ?(1-x)+1/2(x+1)1/?(1-x) mas quando vou derivar novamente y''(x) estou me perdendo no meio dos cálculos e esta ficando cada vez maior poderiam me ajudar.
Desde já agradeço.
-
Maou
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Dez 03, 2014 13:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qua Dez 03, 2014 15:09
por adauto martins » Qua Dez 03, 2014 15:09
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por lucas_carvalho » Qua Dez 03, 2014 15:12
por lucas_carvalho » Qua Dez 03, 2014 15:12
Olá!
Para derivar funções desse tipo precisamos da regra da multiplicação:
[f(x)g(x)]' = f'(x)g(x)+g'(x)f(x)
Então:
![y' =[x+1]' . \sqrt[]{1-x} + (x+1). [\sqrt[]{x-1}]' y' =[x+1]' . \sqrt[]{1-x} + (x+1). [\sqrt[]{x-1}]'](/latexrender/pictures/d3321ca13e0b997bb53c0c96eb04f665.png)
![y'=\sqrt[]{1-x} - \frac{x+1}{2\sqrt[]{1-x}} y'=\sqrt[]{1-x} - \frac{x+1}{2\sqrt[]{1-x}}](/latexrender/pictures/b26987de1767536903a2dd3f0301e509.png)
Agora é só calcular a segunda derivada, lembrado que a derivada de uma subtração é igual a subtração das derivadas:
![y''= [\sqrt[]{1-x}]' -[\frac{x+1}{2\sqrt[]{1-x}}]' y''= [\sqrt[]{1-x}]' -[\frac{x+1}{2\sqrt[]{1-x}}]'](/latexrender/pictures/4a86d40ed83682d06b2d59d945edc230.png)
![y'' = -\frac{1}{2\sqrt[]{1-x}} - \frac{1}{2}. \frac{\sqrt[]{1-x}+\frac{x+1}{2\sqrt[]{1-x}}}{1-x} y'' = -\frac{1}{2\sqrt[]{1-x}} - \frac{1}{2}. \frac{\sqrt[]{1-x}+\frac{x+1}{2\sqrt[]{1-x}}}{1-x}](/latexrender/pictures/c4e585f46c54bb61a05531f9186181e9.png)
![y'' = -\frac{1}{2\sqrt[]{1-x}}- \frac{3-x}{4\sqrt[]{(1-x)^3}} y'' = -\frac{1}{2\sqrt[]{1-x}}- \frac{3-x}{4\sqrt[]{(1-x)^3}}](/latexrender/pictures/2da260342753b73bbcdb12a34eaf7e12.png)
Espero ter ajudado!
-
lucas_carvalho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Dez 02, 2014 20:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derivada de segunda ordem
por lgbmp » Sex Set 03, 2010 19:25
- 2 Respostas
- 3040 Exibições
- Última mensagem por lgbmp

Seg Set 06, 2010 13:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:43
- 2 Respostas
- 2238 Exibições
- Última mensagem por spektroos

Dom Nov 25, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:48
- 1 Respostas
- 1554 Exibições
- Última mensagem por e8group

Dom Nov 25, 2012 10:12
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de segunda ordem
por Fernandobertolaccini » Sex Jul 11, 2014 14:37
- 0 Respostas
- 979 Exibições
- Última mensagem por Fernandobertolaccini

Sex Jul 11, 2014 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de primeira e segunda ordem
por Nina » Qui Nov 05, 2009 20:52
- 1 Respostas
- 4120 Exibições
- Última mensagem por marciommuniz

Sex Nov 06, 2009 13:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![y=(x+1)\sqrt[]{1-x}.... y=(x+1)\sqrt[]{1-x}....](/latexrender/pictures/565688fe13fa37a11a704b304252de71.png) ,vamos usar a derivada do produto,ou seja...(f.g)'=f'.g+fg'...logo...
,vamos usar a derivada do produto,ou seja...(f.g)'=f'.g+fg'...logo...![y'=\sqrt[]{1-x}+(x+1)(1/2)(-1/\sqrt[]{1-x})=\sqrt[]{1-x}-(x+1/2.\sqrt[]{1-x}) y'=\sqrt[]{1-x}+(x+1)(1/2)(-1/\sqrt[]{1-x})=\sqrt[]{1-x}-(x+1/2.\sqrt[]{1-x})](/latexrender/pictures/c20d0ce1c025cd1bb7c33e6e023e5067.png) ...
...![y'=(1-x)-(x+1)/(2.\sqrt[]{1-x})=-2x/(2.\sqrt[]{1-x})=-x/(\sqrt[]{1-x}) y'=(1-x)-(x+1)/(2.\sqrt[]{1-x})=-2x/(2.\sqrt[]{1-x})=-x/(\sqrt[]{1-x})](/latexrender/pictures/5ac0329d4335151ccac6523690f7a459.png) ...aqui agora e usar a derivada do quociente,ou seja...
...aqui agora e usar a derivada do quociente,ou seja...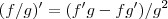 ,entao...
,entao...![y''=((-1).\sqrt[]{1-x}-(-x).(1/2)(-1/\sqrt[]{1-x}))/({\sqrt[]{1-x}})^{2} y''=((-1).\sqrt[]{1-x}-(-x).(1/2)(-1/\sqrt[]{1-x}))/({\sqrt[]{1-x}})^{2}](/latexrender/pictures/06bd6d72e03b1985538da51e0814bb6a.png)
![=-\sqrt[]{1-x}-x/(2.\sqrt[]{1-x}).(1-x)) =-\sqrt[]{1-x}-x/(2.\sqrt[]{1-x}).(1-x))](/latexrender/pictures/151354598db4cb062738e417fd36b9dd.png)
![=-2.({1-x})^{2}-x/(2.\sqrt[]{({1-x})^{3}}) =-2.({1-x})^{2}-x/(2.\sqrt[]{({1-x})^{3}})](/latexrender/pictures/128412d4663d365afdcf42ef10f61749.png)
![=-2(1-2x+{x}^{2})-x/(2.\sqrt[]{({1-x})^{3}}) =-2(1-2x+{x}^{2})-x/(2.\sqrt[]{({1-x})^{3}})](/latexrender/pictures/7dc63ef0342c36a69033816af752afaa.png)
![\Rightarrow y''=-{x}^{2}+x-2/(\sqrt[]{({1-x})^{3}}) \Rightarrow y''=-{x}^{2}+x-2/(\sqrt[]{({1-x})^{3}})](/latexrender/pictures/8fd1df867858a2caa8457bf871fb1974.png)

![y' =[x+1]' . \sqrt[]{1-x} + (x+1). [\sqrt[]{x-1}]' y' =[x+1]' . \sqrt[]{1-x} + (x+1). [\sqrt[]{x-1}]'](/latexrender/pictures/d3321ca13e0b997bb53c0c96eb04f665.png)
![y'=\sqrt[]{1-x} - \frac{x+1}{2\sqrt[]{1-x}} y'=\sqrt[]{1-x} - \frac{x+1}{2\sqrt[]{1-x}}](/latexrender/pictures/b26987de1767536903a2dd3f0301e509.png)
![y''= [\sqrt[]{1-x}]' -[\frac{x+1}{2\sqrt[]{1-x}}]' y''= [\sqrt[]{1-x}]' -[\frac{x+1}{2\sqrt[]{1-x}}]'](/latexrender/pictures/4a86d40ed83682d06b2d59d945edc230.png)
![y'' = -\frac{1}{2\sqrt[]{1-x}} - \frac{1}{2}. \frac{\sqrt[]{1-x}+\frac{x+1}{2\sqrt[]{1-x}}}{1-x} y'' = -\frac{1}{2\sqrt[]{1-x}} - \frac{1}{2}. \frac{\sqrt[]{1-x}+\frac{x+1}{2\sqrt[]{1-x}}}{1-x}](/latexrender/pictures/c4e585f46c54bb61a05531f9186181e9.png)
![y'' = -\frac{1}{2\sqrt[]{1-x}}- \frac{3-x}{4\sqrt[]{(1-x)^3}} y'' = -\frac{1}{2\sqrt[]{1-x}}- \frac{3-x}{4\sqrt[]{(1-x)^3}}](/latexrender/pictures/2da260342753b73bbcdb12a34eaf7e12.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
