eixo radical e o lugar geometrico dos pontos q. sao equipotentes(de mesma potencia)em relaçao a circunferencias nao concentricas...
vamos tomar um ponto P(x,y) do plano q. contem as circunferencias...entao:
PA.PB=PC.PD(potencia de ponto em relaçao as circunferencias),onde A,B sao pontos da circunferencia
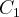
tal q. a reta q. contem PA,PB passam pelo cenro da circunferencia
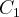
...racionio analogo se faz em relaçao a circunferencia
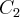
,e os pontos C,D...
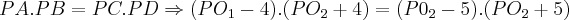
,onde
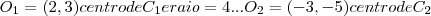
e raio =5...entao:
multiplicando e rearanjandos termos,chegaremos em...
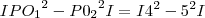
...ondeI(...)I,modulos...calculando e rearranjando os termos chegaremos na equaçao de uma reta(ax+by+c)eq.do eixo radical, q. e perpendicular ao eixo q. uni as duas circunferencias...


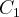 tal q. a reta q. contem PA,PB passam pelo cenro da circunferencia
tal q. a reta q. contem PA,PB passam pelo cenro da circunferencia 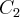 ,e os pontos C,D...
,e os pontos C,D...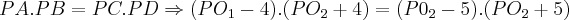 ,onde
,onde 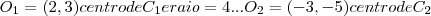 e raio =5...entao:
e raio =5...entao: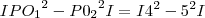 ...ondeI(...)I,modulos...calculando e rearranjando os termos chegaremos na equaçao de uma reta(ax+by+c)eq.do eixo radical, q. e perpendicular ao eixo q. uni as duas circunferencias...
...ondeI(...)I,modulos...calculando e rearranjando os termos chegaremos na equaçao de uma reta(ax+by+c)eq.do eixo radical, q. e perpendicular ao eixo q. uni as duas circunferencias...
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.