 por iceman » Sáb Nov 22, 2014 13:44
por iceman » Sáb Nov 22, 2014 13:44
Se
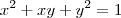
,encontre
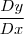
Agradeço pela ajuda!

-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por adauto martins » Sáb Nov 22, 2014 15:37
por adauto martins » Sáb Nov 22, 2014 15:37
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por iceman » Sáb Nov 22, 2014 16:08
por iceman » Sáb Nov 22, 2014 16:08
adauto martins escreveu: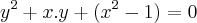
...
![y=-x+\sqrt[]{4-3x}/2 y=-x+\sqrt[]{4-3x}/2](/latexrender/pictures/5fabb065f0c86a1fa3e5b894cc6742e3.png)
,ou
![y=-x-\sqrt[]{4-3x}/2 y=-x-\sqrt[]{4-3x}/2](/latexrender/pictures/d4b61b2ae6721c85c5b1288484799ed9.png)
1)
![dy/dx=-1+((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}+3)/(\sqrt[]{4-3x}) dy/dx=-1+((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}+3)/(\sqrt[]{4-3x})](/latexrender/pictures/7fcb8cfd52f582cc2e762888fd0fd805.png)
2)
![dy/dx=-1-((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}-3)/(\sqrt[]{4-3x}) dy/dx=-1-((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}-3)/(\sqrt[]{4-3x})](/latexrender/pictures/6551e45b643f3441e063b42990fd3998.png)
entendi nada
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Sáb Nov 22, 2014 18:51
por Cleyson007 » Sáb Nov 22, 2014 18:51
Boa tarde iceman!
Utilizando derivação implícita. Veja:
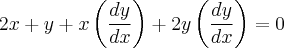
Colocando o
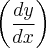
em evidência, temos:
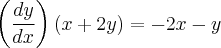
Logo,
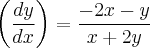
Comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por adauto martins » Dom Nov 23, 2014 12:36
por adauto martins » Dom Nov 23, 2014 12:36
a soluçao do cleyson e a correta...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada - Questão
por iceman » Dom Set 16, 2012 16:37
- 3 Respostas
- 1735 Exibições
- Última mensagem por iceman

Dom Set 16, 2012 19:59
Cálculo: Limites, Derivadas e Integrais
-
- Re: Derivada - Questão
por iceman » Dom Set 16, 2012 23:06
- 2 Respostas
- 1348 Exibições
- Última mensagem por Russman

Seg Set 17, 2012 11:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - Questão
por iceman » Ter Set 18, 2012 18:56
- 3 Respostas
- 1915 Exibições
- Última mensagem por Renato_RJ

Ter Set 18, 2012 19:24
Cálculo: Limites, Derivadas e Integrais
-
- [DUVIDA] Questão de Derivada.
por Jefferson_mcz » Sex Mai 17, 2013 00:21
- 0 Respostas
- 1741 Exibições
- Última mensagem por Jefferson_mcz

Sex Mai 17, 2013 00:21
Cálculo: Limites, Derivadas e Integrais
-
- Derivada-questão da prova
por johnatta » Ter Jun 16, 2015 13:47
- 1 Respostas
- 2232 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 27, 2015 15:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
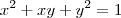 ,encontre
,encontre 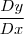


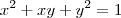 ,encontre
,encontre 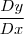


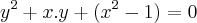 ...
...![y=-x+\sqrt[]{4-3x}/2 y=-x+\sqrt[]{4-3x}/2](/latexrender/pictures/5fabb065f0c86a1fa3e5b894cc6742e3.png) ,ou
,ou ![y=-x-\sqrt[]{4-3x}/2 y=-x-\sqrt[]{4-3x}/2](/latexrender/pictures/d4b61b2ae6721c85c5b1288484799ed9.png)
![dy/dx=-1+((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}+3)/(\sqrt[]{4-3x}) dy/dx=-1+((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}+3)/(\sqrt[]{4-3x})](/latexrender/pictures/7fcb8cfd52f582cc2e762888fd0fd805.png)
![dy/dx=-1-((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}-3)/(\sqrt[]{4-3x}) dy/dx=-1-((3/4)/\sqrt[]{4-3x}))=(-4\sqrt[]{4-3x}-3)/(\sqrt[]{4-3x})](/latexrender/pictures/6551e45b643f3441e063b42990fd3998.png)

...
,ou

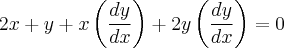
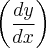 em evidência, temos:
em evidência, temos: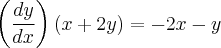
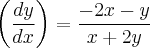



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)