dados os vetores u=(4,1,2), v=(0,3,8), w=(3,1,2)
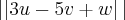
estou com duvida se fica:
|3| ||u||+|-5| ||v||+|1| ||w|| pela propriedade ||ku||=|k| ||u||
ou se multiplica os vetores normalmente e fica assim:
3(4,1,2)-5(0,3,8)+(3,1,2)
(12,3,6)-(0,15,8)+(3,1,2)...
por nandooliver008 » Qua Nov 12, 2014 00:51
Voltar para Geometria Analítica
por amigao » Sex Mai 09, 2014 16:37
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
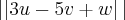
![\left|v \right|=\sqrt[]{{x}^{2}+{y}^{2}+...+{z}^{2}}](/latexrender/pictures/510b9e9623ea1a2a2202f925a3a655bb.png "\left|v \right|=\sqrt[]{{x}^{2}+{y}^{2}+...+{z}^{2}}")
p/v=(x,y,..,z)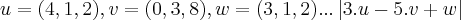
=
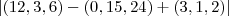=![\left|(15,-10,-16 )\right|=\sqrt[]{{15}^{2}+({-10})^{2}+({-16})^{2}}=\sqrt[]{581}](/latexrender/pictures/6dfdebc01a6b6246af1256e829cb4b19.png "\left|(15,-10,-16 )\right|=\sqrt[]{{15}^{2}+({-10})^{2}+({-16})^{2}}=\sqrt[]{581}")
..