 por GMAT2010 » Ter Jan 05, 2010 21:07
por GMAT2010 » Ter Jan 05, 2010 21:07
Errei esta questão em um simulado que fiz recentemente. Anotei a resposta certa em algum lugar, mas não consigo encontrar mais ela... Gostaria muito que alguém dissesse se encontrei a maneira de resolver ou, caso esteja errado, qual a maneira certa.
O enunciado da questão é: Em um grupo de 20 astronautas, existem 12 com experiência de vôo. Quantos grupos de 3 astronautas podem ser formados, contendo pelo menos uma pessoa com experiência?
A solução que encontrei são 3 combinações. Ou todos os 3 astronautas têm experiência, ou 2 tem e um não tem, ou um tem e dois não tem.
O resultado seria então: C12,3 + C12,2 x 8 + C8,2 x 12
= 12!/(3!(12-3)! + [12!/(2!(12-2)! x 8] + [8!/(2!(8-2)! x 12]
= 220 + 528 + 336 = 1084
Estou certo ou errado?
Muito obrigado pela ajuda
-
GMAT2010
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 05, 2010 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng de Produção
- Andamento: formado
 por MarceloFantini » Ter Jan 05, 2010 23:32
por MarceloFantini » Ter Jan 05, 2010 23:32
Boa noite!
Confesso que não sou muito bom em Análise Combinátoria, mas considerei a questão desta maneira:
Para que tenha
pelo menos um com experiência, é mais fácil pegar todos os grupos de 3 astronautas e retirar os grupos os quais não tem
nenhum com experiência. Logo:
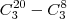
.
Fazendo as contas, cheguei em 1024. É essa a resposta?
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por GMAT2010 » Qua Jan 06, 2010 21:16
por GMAT2010 » Qua Jan 06, 2010 21:16
Fantini,
Obrigado pela dica. Realmente é mais rápido resolver desta maneira.
Fiz essa conta, e continuo chegando no mesmo resultado: 1084.
Estou errando em algum lugar? Será que realmente é esta a maneira de resolver esta questão?
-
GMAT2010
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 05, 2010 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng de Produção
- Andamento: formado
 por MarceloFantini » Qua Jan 06, 2010 22:32
por MarceloFantini » Qua Jan 06, 2010 22:32
Boa noite!
Cara, desculpe. Sua resposta está certa, errei nas contas.
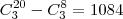
, conforme o seu resultado. Foi erro da minha parte!
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- mediana...não consigo acertar
por TEKA » Seg Mar 29, 2010 11:38
- 1 Respostas
- 3398 Exibições
- Última mensagem por Neperiano

Sex Set 17, 2010 15:36
Estatística
-
- Chance acertar 3 dezenas mega sena
por alezeit » Qui Jan 02, 2014 12:53
- 1 Respostas
- 3280 Exibições
- Última mensagem por Baltuilhe

Dom Jan 21, 2018 03:55
Probabilidade
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3156 Exibições
- Última mensagem por Jesicaa

Dom Mar 15, 2015 00:06
Sistemas de Equações
-
- E agora? Dúvida em limites
por Cleyson007 » Sáb Jun 09, 2012 16:24
- 3 Respostas
- 2301 Exibições
- Última mensagem por MarceloFantini

Dom Jun 10, 2012 15:30
Cálculo: Limites, Derivadas e Integrais
-
- Quebrando a cabeça ate agora :/
por Amandatkm » Dom Abr 28, 2013 17:48
- 8 Respostas
- 4207 Exibições
- Última mensagem por Amandatkm

Ter Abr 30, 2013 15:03
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


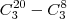 .
.

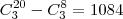 , conforme o seu resultado. Foi erro da minha parte!
, conforme o seu resultado. Foi erro da minha parte!