 por felipederaldino » Qua Nov 05, 2014 23:36
por felipederaldino » Qua Nov 05, 2014 23:36
to com dificuldade pra entender o enunciado e resolve esse problemaa
A raiz quadrada aproximada de um número real positivo P pode ser calculada por meio do seguinte método:
- Escolhe-se um número real positivo a0;
- Obtém-se uma sequência de números cujo termo geral é dado por
![{a}_{n+1}=\frac{1}{2}\left[{a}_{n} + \frac{P}{{a}_{n}}\right] {a}_{n+1}=\frac{1}{2}\left[{a}_{n} + \frac{P}{{a}_{n}}\right]](/latexrender/pictures/4d7851317e060d2a28d4a9b839b8a3c8.png)
, sendo
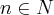
.
À medida que n aumenta, an+1 representará aproximações para a raiz quadrada procurada. Admitindo P = 2, a0 = 4 e utilizando o método acima descrito, pode-se afirmar que o valor da segunda aproximação (a2) de com duas casas decimais e sem arredondamento, é:
( ) 1,56
( ) 1,52
( ) 1,53
( ) 1,54
( ) 1,55
-
felipederaldino
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Nov 05, 2014 17:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ufmt)...
por willwgo » Qua Jun 29, 2011 16:49
- 4 Respostas
- 2683 Exibições
- Última mensagem por willwgo

Seg Jul 04, 2011 16:50
Geometria Plana
-
- questão função
por sheila » Qui Set 06, 2007 22:37
- 4 Respostas
- 7830 Exibições
- Última mensagem por admin

Ter Set 11, 2007 16:39
Funções
-
- Questão de Funçao
por kael » Qui Mar 05, 2009 16:30
- 4 Respostas
- 2995 Exibições
- Última mensagem por Molina

Sex Mar 06, 2009 12:47
Funções
-
- Questao de Funçao
por leilahomsi » Qua Jan 09, 2013 19:19
- 1 Respostas
- 1316 Exibições
- Última mensagem por e8group

Qua Jan 09, 2013 22:38
Funções
-
- [Questão de Função]
por zanotto » Sex Mar 21, 2014 23:18
- 3 Respostas
- 2230 Exibições
- Última mensagem por Russman

Sáb Mar 22, 2014 01:22
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{a}_{n+1}=\frac{1}{2}\left[{a}_{n} + \frac{P}{{a}_{n}}\right] {a}_{n+1}=\frac{1}{2}\left[{a}_{n} + \frac{P}{{a}_{n}}\right]](/latexrender/pictures/4d7851317e060d2a28d4a9b839b8a3c8.png) , sendo
, sendo 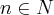 .
.

![{a}_{0+1}=(1/2)[4+(2/4)]=9/4...{a}_{1}=9/4 {a}_{0+1}=(1/2)[4+(2/4)]=9/4...{a}_{1}=9/4](/latexrender/pictures/8c5db88a3d79a106fa9193e301af21bc.png) ...
...![{a}_{2}={a}_{1+1}=(1/2)[(9/4)+(2/(9/4))]=(1/2)[(9/4)+(8/9)]=113/72\simeq1.56 {a}_{2}={a}_{1+1}=(1/2)[(9/4)+(2/(9/4))]=(1/2)[(9/4)+(8/9)]=113/72\simeq1.56](/latexrender/pictures/e42fdf096adc3dde100b523cea00e244.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.