A raiz quadrada aproximada de um número real positivo P pode ser calculada por meio do seguinte método:
- Escolhe-se um número real positivo a0;
- Obtém-se uma sequência de números cujo termo geral é dado por
![{a}_{n+1}=\frac{1}{2}\left[{a}_{n} + \frac{P}{{a}_{n}}\right]](/latexrender/pictures/4d7851317e060d2a28d4a9b839b8a3c8.png "{a}_{n+1}=\frac{1}{2}\left[{a}_{n} + \frac{P}{{a}_{n}}\right]")
, sendo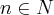 
.À medida que n aumenta, an+1 representará aproximações para a raiz quadrada procurada. Admitindo P = 2, a0 = 4 e utilizando o método acima descrito, pode-se afirmar que o valor da segunda aproximação (a2) de com duas casas decimais e sem arredondamento, é:
( ) 1,56
( ) 1,52
( ) 1,53
( ) 1,54
( ) 1,55
![{a}_{0+1}=(1/2)[4+(2/4)]=9/4...{a}_{1}=9/4](/latexrender/pictures/8c5db88a3d79a106fa9193e301af21bc.png "{a}_{0+1}=(1/2)[4+(2/4)]=9/4...{a}_{1}=9/4")
...![{a}_{2}={a}_{1+1}=(1/2)[(9/4)+(2/(9/4))]=(1/2)[(9/4)+(8/9)]=113/72\simeq1.56](/latexrender/pictures/e42fdf096adc3dde100b523cea00e244.png "{a}_{2}={a}_{1+1}=(1/2)[(9/4)+(2/(9/4))]=(1/2)[(9/4)+(8/9)]=113/72\simeq1.56")
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)