 por Mateus Mataveli » Qui Nov 06, 2014 00:39
por Mateus Mataveli » Qui Nov 06, 2014 00:39
Oi gente, por favor me ajudem neste exercício, ele é simples, porém nao consigo entender como se desenvolve, olhei algumas explicações mas acabei me confundindo ainda mais. O exercício é o seguinte:
O algarismo das unidades de 2013^2014 (2013 elevado a 2014) é:
a) 1
B) 3
C) 4
d) 7
E) 9
Existe alguma formula? Desde ja agradeço!
-
Mateus Mataveli
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 06, 2014 00:27
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Tecnico Mecânico
- Andamento: cursando
 por adauto martins » Sex Nov 07, 2014 10:21
por adauto martins » Sex Nov 07, 2014 10:21
para resolver esse exercicio teremos q. primeiro provar:
9 elevado a uma potencia par,tera na casa das unidades o numero 1...9 elevado a uma potencia impar,tera na casa das unidades o numero 9...fica como exercicio a prova...vamos a soluçao:
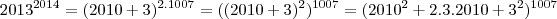
=
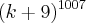
,expandindo a expressao em um binomio de newto,teremos:
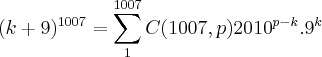
,onde C(1007,K)=1007!/(k!(1007-k)!)...logo teremos:
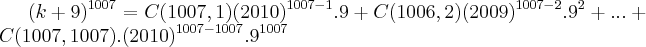
,como 1007 e um numero impar,entao a casa das unidades tera o numero 9...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Mateus Mataveli » Sex Nov 07, 2014 17:23
por Mateus Mataveli » Sex Nov 07, 2014 17:23
Nao existe uma forma mais simples?
-
Mateus Mataveli
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 06, 2014 00:27
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Tecnico Mecânico
- Andamento: cursando
 por adauto martins » Sáb Nov 08, 2014 10:08
por adauto martins » Sáb Nov 08, 2014 10:08
caro matheus,
se tem eu nao conheço...mas no estudo de criterios de divisibilidade vc pode encontrar muito para soluçao de exercicios assim...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2291 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1734 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3738 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2022 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- POTENCIACAO
por CaAtr » Ter Mar 09, 2010 20:23
- 3 Respostas
- 2292 Exibições
- Última mensagem por CaAtr

Ter Mar 09, 2010 22:17
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


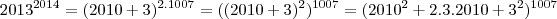 =
=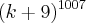 ,expandindo a expressao em um binomio de newto,teremos:
,expandindo a expressao em um binomio de newto,teremos: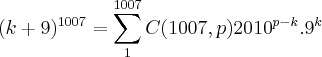 ,onde C(1007,K)=1007!/(k!(1007-k)!)...logo teremos:
,onde C(1007,K)=1007!/(k!(1007-k)!)...logo teremos: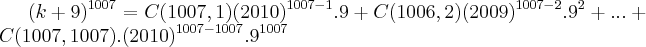 ,como 1007 e um numero impar,entao a casa das unidades tera o numero 9...
,como 1007 e um numero impar,entao a casa das unidades tera o numero 9...