 por juliohenriquelima14 » Ter Nov 04, 2014 11:24
por juliohenriquelima14 » Ter Nov 04, 2014 11:24
Bom dia pessoal!
Sou novo aqui no fórum, por isso ainda estou meio perdido. Primeiramente me desculpem se houver algum equivoco na postagem.
Pois bem, tenho a seguinte questão de indução matemática para resolver, consegui chegar tranquilo até o terceiro passo. Lá tem uma parte, inclusive
eu até destaquei no anexo. Eu venho pedir a ajuda de vocês para que possam analisar meu feito e fazer a devida correção se caso precisar.
Obrigado pela atenção de todos.
- Anexos
-
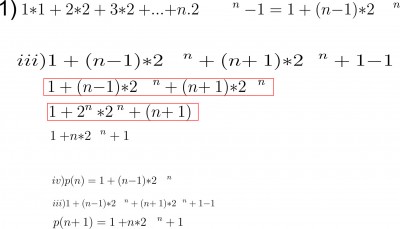
- inducMatematica
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
 por Russman » Ter Nov 04, 2014 13:53
por Russman » Ter Nov 04, 2014 13:53
Esta bastante confuso de entender o que você quer/está fazendo. Explique o problema.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por juliohenriquelima14 » Ter Nov 04, 2014 14:07
por juliohenriquelima14 » Ter Nov 04, 2014 14:07
Boa tarde amigo!
Eu preciso provar por induçao a validação a equação acima
1*1+2*2¹+3*2²+...+n.2^n-1 = 1+(n-1)*2^n
Eu tenho que provar que o resultado do segundo passo vai ser igual ao resultado do terceiro passo.
Só que é exatamente onde eu estou me confundindo não consigo resolver a parte do anexo que está destacada.
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
 por juliohenriquelima14 » Ter Nov 04, 2014 14:08
por juliohenriquelima14 » Ter Nov 04, 2014 14:08
Tentei fazer da forma acima como está no anexo, mas não sei se está correto.
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
 por Russman » Ter Nov 04, 2014 15:55
por Russman » Ter Nov 04, 2014 15:55
Agora sim! (:
A afirmação que queremos provar é
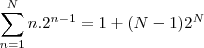
Vou chamar
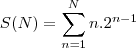
.
Bem, o 1° passo da prova por indução é verificar que( como a soma começa em

) a afirmação é verdadeira para
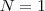
. De fato,
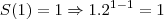
Perfeito. Agora precisamos mostrar que a afirmação é válida para N+1.
Veja que
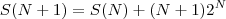
Mas, por hipótese,
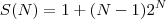
. Assim,
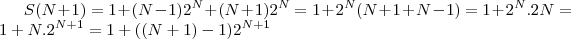
Daí, trocando N+1 por N temos
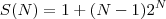
que é a hipótese inicial.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Ter Nov 04, 2014 16:09
por Russman » Ter Nov 04, 2014 16:09
Mais um comentário.
Não é difícil mostrar que , de fato,
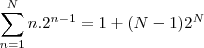
.
Considere as somas
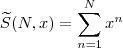
e
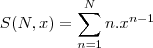
.
OBS: A sua soma de interesse é
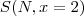
Note que
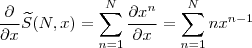
ou seja,
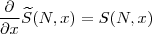
.
Assim, como sabemos que
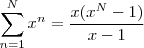
, (não nos preocupemos com o caso x=1), então
![S(N,x) = \frac{\partial }{\partial x} \frac{x(x^N-1)}{x-1} = \frac{1}{(x-1)^2} [x^N(N(x-1)-1)+1] S(N,x) = \frac{\partial }{\partial x} \frac{x(x^N-1)}{x-1} = \frac{1}{(x-1)^2} [x^N(N(x-1)-1)+1]](/latexrender/pictures/6d4d4a5f31a6b5daa94da51f0ecc3ab6.png)
Daí, fazendo

temos
![S(N,x=2) = \frac{1}{(2-1)^2} [2^N(N(2-1)-1)+1] = 1. [2^N(N.1-1)+1)] = 2^N(N-1) + 1 S(N,x=2) = \frac{1}{(2-1)^2} [2^N(N(2-1)-1)+1] = 1. [2^N(N.1-1)+1)] = 2^N(N-1) + 1](/latexrender/pictures/e4a838575b78fb29334c8c0332adc5bc.png)
que é a afirmação que você gostaria de provar por indução.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por juliohenriquelima14 » Ter Nov 04, 2014 16:28
por juliohenriquelima14 » Ter Nov 04, 2014 16:28
Bom!!! É isso mesmo que a questão pede. Muito bom, com vocês consegui clarear bastante o entendimento.
Muito grato!
-
juliohenriquelima14
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Nov 01, 2014 09:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema da Informação
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas]Duvida nessa questão
por Flavio50 » Dom Abr 19, 2015 12:45
- 2 Respostas
- 1901 Exibições
- Última mensagem por Flavio50

Seg Abr 27, 2015 13:47
Cálculo: Limites, Derivadas e Integrais
-
- [Método de Newton] - Duvida nessa questão
por zifles2012 » Seg Set 17, 2012 16:13
- 1 Respostas
- 2141 Exibições
- Última mensagem por LuizAquino

Seg Set 17, 2012 19:55
Cálculo Numérico e Aplicações
-
- ajuda nessa questão
 por zenildo » Dom Jun 05, 2016 23:36
por zenildo » Dom Jun 05, 2016 23:36
- 4 Respostas
- 4986 Exibições
- Última mensagem por Thiago1986Iz

Dom Jul 17, 2016 17:07
Trigonometria
-
- [porcentagem] Ajudem nessa questão?
por amanda s » Sex Nov 15, 2013 20:20
- 2 Respostas
- 3520 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 01:04
Conversão de Unidades
-
- [logica] Ajudem nessa questão
por amanda s » Sáb Nov 16, 2013 09:56
- 1 Respostas
- 1614 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 14:56
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



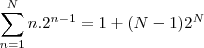
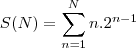 .
. ) a afirmação é verdadeira para
) a afirmação é verdadeira para 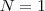 . De fato,
. De fato,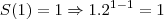
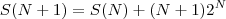
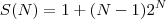 . Assim,
. Assim, 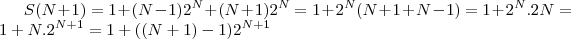
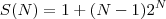
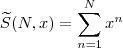 e
e 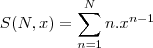 .
.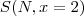
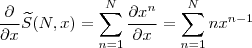
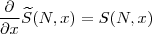 .
.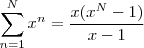 , (não nos preocupemos com o caso x=1), então
, (não nos preocupemos com o caso x=1), então![S(N,x) = \frac{\partial }{\partial x} \frac{x(x^N-1)}{x-1} = \frac{1}{(x-1)^2} [x^N(N(x-1)-1)+1] S(N,x) = \frac{\partial }{\partial x} \frac{x(x^N-1)}{x-1} = \frac{1}{(x-1)^2} [x^N(N(x-1)-1)+1]](/latexrender/pictures/6d4d4a5f31a6b5daa94da51f0ecc3ab6.png)
 temos
temos![S(N,x=2) = \frac{1}{(2-1)^2} [2^N(N(2-1)-1)+1] = 1. [2^N(N.1-1)+1)] = 2^N(N-1) + 1 S(N,x=2) = \frac{1}{(2-1)^2} [2^N(N(2-1)-1)+1] = 1. [2^N(N.1-1)+1)] = 2^N(N-1) + 1](/latexrender/pictures/e4a838575b78fb29334c8c0332adc5bc.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.