 por Lais-Lima » Seg Out 27, 2014 16:15
por Lais-Lima » Seg Out 27, 2014 16:15
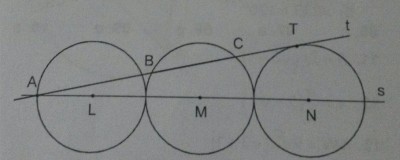
As circunferências da figura têm raios iguais a 5, seus centros estão na reta s e a circunferência de centro M tangencia as outras duas. A reta t é tangente à circunferência de centro N e passa pelo ponto A, em que a reta s intersecta a circunferência de centro L. Calcule o comprimento da corda BC, que a reta t determina na circunferência de centro M.
Formei o triângulo ATN, retângulo em T.
Sei que o lado AN mede 25 e o lado TN mede 5.
25² = 5² + AT²
625 - 25 = AT²
AT =
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
600 = 10
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
6
E agora?
O gabarito é BC = 8.
- Anexos
-
-
Lais-Lima
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Set 13, 2014 12:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Qui Out 30, 2014 11:39
por adauto martins » Qui Out 30, 2014 11:39
seja

o angulo mais agulo do triang.ATN,logo
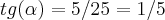
...temos q. AB.AC=10.20=200...
vamos tomar o triang.ACM, e aplicar a lei dos cossenos,entao...
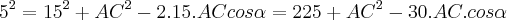
...
temos q.
![tg\alpha=1/5\Rightarrow sen\alpha=cos\alpha/5\Rightarrow {cos\alpha}^{2}+({cos\alpha/5})^{2}=1\Rightarrow cos\alpha=5/\sqrt[]{26} tg\alpha=1/5\Rightarrow sen\alpha=cos\alpha/5\Rightarrow {cos\alpha}^{2}+({cos\alpha/5})^{2}=1\Rightarrow cos\alpha=5/\sqrt[]{26}](/latexrender/pictures/6eacd9faf39b4b1dd713cc9cab85fab8.png)
...entao,
![25=225+{AC}^{2}+30AC.(5/\sqrt[]{26})\Rightarrow {AC}^{2}-(150/\sqrt[]{26})AC+200=0 25=225+{AC}^{2}+30AC.(5/\sqrt[]{26})\Rightarrow {AC}^{2}-(150/\sqrt[]{26})AC+200=0](/latexrender/pictures/07dbfabdccdea3a52198ccfe071eeab0.png)
...cujas soluçoes sao AC

18.95 OU AC

10.55(q. nao pode ser soluçao pois,
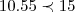
)...logo temos AB.AC=200 e AB+BC=18.95...logo
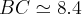
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 600 = 10
600 = 10![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 6
6
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 600 = 10
600 = 10![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 6
6
 o angulo mais agulo do triang.ATN,logo
o angulo mais agulo do triang.ATN,logo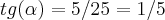 ...temos q. AB.AC=10.20=200...
...temos q. AB.AC=10.20=200...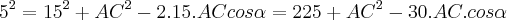 ...
...![tg\alpha=1/5\Rightarrow sen\alpha=cos\alpha/5\Rightarrow {cos\alpha}^{2}+({cos\alpha/5})^{2}=1\Rightarrow cos\alpha=5/\sqrt[]{26} tg\alpha=1/5\Rightarrow sen\alpha=cos\alpha/5\Rightarrow {cos\alpha}^{2}+({cos\alpha/5})^{2}=1\Rightarrow cos\alpha=5/\sqrt[]{26}](/latexrender/pictures/6eacd9faf39b4b1dd713cc9cab85fab8.png) ...entao,
...entao, ![25=225+{AC}^{2}+30AC.(5/\sqrt[]{26})\Rightarrow {AC}^{2}-(150/\sqrt[]{26})AC+200=0 25=225+{AC}^{2}+30AC.(5/\sqrt[]{26})\Rightarrow {AC}^{2}-(150/\sqrt[]{26})AC+200=0](/latexrender/pictures/07dbfabdccdea3a52198ccfe071eeab0.png) ...cujas soluçoes sao AC
...cujas soluçoes sao AC 18.95 OU AC
18.95 OU AC 10.55(q. nao pode ser soluçao pois,
10.55(q. nao pode ser soluçao pois,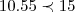 )...logo temos AB.AC=200 e AB+BC=18.95...logo
)...logo temos AB.AC=200 e AB+BC=18.95...logo 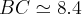



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.