 por Uesley Junior » Sex Out 10, 2014 14:53
por Uesley Junior » Sex Out 10, 2014 14:53
Para destacar a importância de trabalhar com sistemas de equações não lineares, vamos levantar a situação em que existe a necessidade de realizar a análise do comportamento de um regime permanente do circuito não linear, quando os valores de tensão através dos resistores podem ser obtidos através da resolução de um sistema de equações não lineares, e o problema se reduz a encontrar uma raiz para o sistema de equações. Uma segunda situação permite mencionar que, no sistema aéreo, os controladores de voo trabalham com radares e, quando dois destes radares estão localizados em posições conhecidas, eles podem determinar a distância de suas localizações até uma aeronave que está se aproximando dentro do espaço aéreo. Neste caso, também temos um sistema de equações não lineares, e a solução está em calcular o valor das raízes das equações. Assim, efetue os seguintes cálculos:
Dado o sistema de equações não lineares:
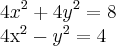
faça uma análise do sistema e, na sequência, assinale a alternativa CORRETA:
a - As derivadas parciais das duas funções que compõem o sistema apresentam ponto de descontinuidade.
b - No sistema, as variáveis x e y assumem o mesmo valor.
c - O Método de Newton é apropriado para calcular o erro relativo das variáveis com referência às raízes de ambas as funções.
d - As duas funções que compõem o sistema apresentam ponto de descontinuidade.
-
Uesley Junior
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Out 10, 2014 13:13
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Sex Out 10, 2014 18:55
por adauto martins » Sex Out 10, 2014 18:55
as soluçao do sistema sao:
(2
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png)
)/5,
![\sqrt[2]{6}/5 \sqrt[2]{6}/5](/latexrender/pictures/202e3a5ca87f6f4427bc85d3e4dc377c.png)
),(-
![2(\sqrt[2]{5})/5 2(\sqrt[2]{5})/5](/latexrender/pictures/90f58da7be80c4fa3706a892c4d24ae8.png)
,
![(\sqrt[2]{6})/5 (\sqrt[2]{6})/5](/latexrender/pictures/3dc979df27ad17edb4e4971d74ee2aa0.png)
),
![-2(\sqrt[2]{5})/5 -2(\sqrt[2]{5})/5](/latexrender/pictures/1ce777c581640a126179528f89096b4b.png)
,
![-(\sqrt[2]{6})/5 -(\sqrt[2]{6})/5](/latexrender/pictures/15c2774ba51a36b690a11272f33170e4.png)
),(
![2(\sqrt[2]{5})/5 2(\sqrt[2]{5})/5](/latexrender/pictures/90f58da7be80c4fa3706a892c4d24ae8.png)
,
![-(\sqrt[2]{6})/5 -(\sqrt[2]{6})/5](/latexrender/pictures/15c2774ba51a36b690a11272f33170e4.png)
),portanto nao apresenta pontos de descontinuidade...suas derivadas parciais tem como soluçoes a origem(0,0),entao nao apresentam pontos de descontinuidades...logo a letra c) e a resposta do exercicio...agora e desenvolver o sistema no metodo de newton e verificar o erro...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] - Matriz de uma trasnformacao linear, Ajuda
por rodrigojuara » Dom Nov 30, 2014 15:05
- 1 Respostas
- 8159 Exibições
- Última mensagem por adauto martins

Seg Dez 01, 2014 16:12
Álgebra Linear
-
- algebra linear ajuda
por gutorocher » Sáb Set 18, 2010 22:36
- 3 Respostas
- 2177 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:31
Álgebra Linear
-
- Geometria Analitica e Algebra linear-O plano - Ajuda
por Danizinhalacerda13 » Qui Mai 01, 2014 20:37
- 3 Respostas
- 2428 Exibições
- Última mensagem por Cleyson007

Sáb Mai 03, 2014 10:15
Geometria Analítica
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10533 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11565 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
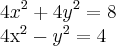


![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) )/5,
)/5,![\sqrt[2]{6}/5 \sqrt[2]{6}/5](/latexrender/pictures/202e3a5ca87f6f4427bc85d3e4dc377c.png) ),(-
),(-![2(\sqrt[2]{5})/5 2(\sqrt[2]{5})/5](/latexrender/pictures/90f58da7be80c4fa3706a892c4d24ae8.png) ,
,![(\sqrt[2]{6})/5 (\sqrt[2]{6})/5](/latexrender/pictures/3dc979df27ad17edb4e4971d74ee2aa0.png) ),
),![-2(\sqrt[2]{5})/5 -2(\sqrt[2]{5})/5](/latexrender/pictures/1ce777c581640a126179528f89096b4b.png) ,
,![-(\sqrt[2]{6})/5 -(\sqrt[2]{6})/5](/latexrender/pictures/15c2774ba51a36b690a11272f33170e4.png) ),(
),(





