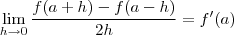


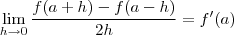

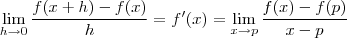 ;
;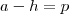 por conseguinte
por conseguinte 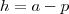 , então:
, então: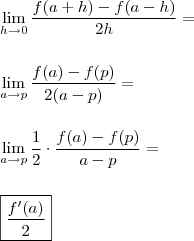

 , defina
, defina 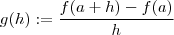 . Dizer que
. Dizer que 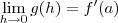 equivale dizer que para qualquer
equivale dizer que para qualquer 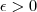 dado , existe
dado , existe 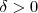 (correspondente ) tal que se
(correspondente ) tal que se 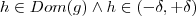 então
então 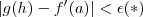 .
. ![\frac{f(a+h) -f(a-h) }{2h} -f'(a) = \frac{f(a+h) -f(a) -(f(a-h) -f(a)) }{2h} -f'(a) = g(h) - \frac{f(a +(-h) ) -f(a)}{2h} -f'(a) = \frac{1}{2} \left[ g(h) - f'(a) - g(-h) - f'(a) \right] \frac{f(a+h) -f(a-h) }{2h} -f'(a) = \frac{f(a+h) -f(a) -(f(a-h) -f(a)) }{2h} -f'(a) = g(h) - \frac{f(a +(-h) ) -f(a)}{2h} -f'(a) = \frac{1}{2} \left[ g(h) - f'(a) - g(-h) - f'(a) \right]](/latexrender/pictures/b84640858021fb205aac98b2736dbc3d.png) .
.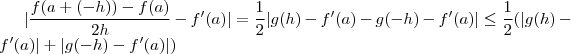 .
. 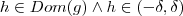 então
então 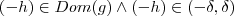 . Desta forma , obtemos que ambas quantidades
. Desta forma , obtemos que ambas quantidades 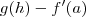 e
e 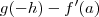 são limitadas por
são limitadas por  e por isso
e por isso 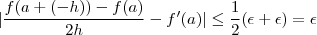 o que prova formalmente que o limite
o que prova formalmente que o limite 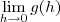 existe e vale
existe e vale 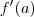 .
. 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: