Se ( 3 - x , x , raiz quadrada de 9 - x ) é uma progressão aritmética, seu 6° termo é ?
Estou com dúvida na parte da álgebra.





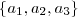 é verdade que, se
é verdade que, se  for sua razão,
for sua razão,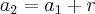
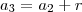
 , temos
, temos
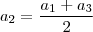
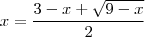
 . Tente resolver. Eu calculei
. Tente resolver. Eu calculei 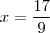 .
.

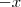 somando e o 3 subtraindo. Ou seja,
somando e o 3 subtraindo. Ou seja, 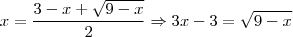
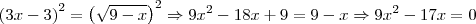
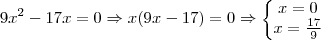
 , a P.A. é
, a P.A. é  . Repare que escolhemos a raíz negativa de
. Repare que escolhemos a raíz negativa de 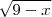 já que para ir de 3 a 0 é necessário subtrair 3 de 3. Assim, para calcular o 3° termo precisamos também subtrair 3 de 0 que dá -3.
já que para ir de 3 a 0 é necessário subtrair 3 de 3. Assim, para calcular o 3° termo precisamos também subtrair 3 de 0 que dá -3.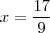 a P.A. é
a P.A. é 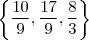 . Aqui, a razão é positiva.
. Aqui, a razão é positiva.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

