Estou precisando de uma ajudinha pois tenho prova esta segunda e estou fazendo os exercícios de algumas provas antigas do professor porém não tenho as respostas das questões e, como ainda não estou dominando a matéria, gostaria que vocês confirmassem a resolução minha ou a corrigissem se for o caso.
tenho a função f(x) =
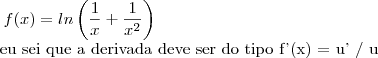
Daí fiz a função se tornar
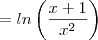
Segui então a substituição e aplicação da derivada da seguinte forma:
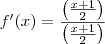 (derivada da fração superior sobre a fração inferior) e cheguei no seguinte resultado:
(derivada da fração superior sobre a fração inferior) e cheguei no seguinte resultado:
Está correta?
Qualquer dúvida no procedimento realizado por mim é só postar!
Abraços e desde já muito obrigado pela prontidão e parabéns ao fórum....


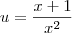
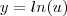
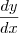 fica:
fica: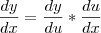




 .
.
 :
: