Exemplo:
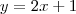
Eu substituí o y por x e o x por y ficando assim:
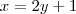
Resolução:
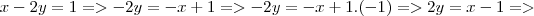
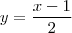
Ai estava eu pesquisando algumas coisas vi isso em um site.
Para determinar a função inversa de f(x)=2x+1 basta:
y=2x+1 (trocar x por y)
x=2y+1 (isolar o y)
-2y= – x+1 (O +1 não deveria virar -1)?
2y= x+1 ( COMO PODE ISSO?)
y=(x+1)/2
f-¹(x)=(x+1)/2
Em meu livro também tem um parecido:
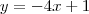
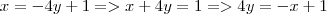
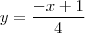
no livro o resultado é
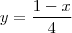
Desde já agradeço.


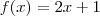
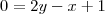
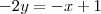
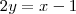
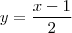

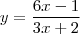
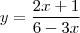
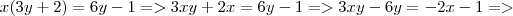
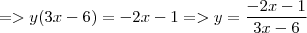
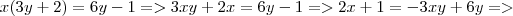
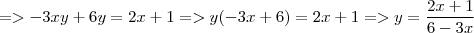


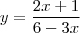

 .
.
 :
: