"Se o logaritmo decimal de 7,5 é 0,875, o número de algarismos d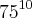e
é:"O gabarito é 19.
Eu desenvolvi o log de 75 e tal e achei 18,75, mas no gabarito ele fala que 18 é característica desse logaritmo e que, portanto
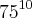é 18+1 = 19.Não entendi de onde saiu esse um e que característica é essa. Agradeço se puderem me ajudar porque só falta esse exercício pra eu terminar minha lista de log.
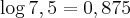e fazes chegar até 
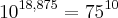, que é o que aparece no enunciado. Ora, 
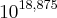é um número com 18 casas decimais depois da vírgula, então os algarismos são esses tais 18 mais o que está à esquerda da vírgula, daí ser 18+1
.
: