 por SauloRJ » Ter Mai 27, 2014 14:25
por SauloRJ » Ter Mai 27, 2014 14:25
Boa Tarde amigos do fórum!
Estou com dúvida na seguinte questão:
(UF.GO) O conjunto-solução da inequação
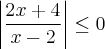
é:
a)
{x ? ? : x = -2}b)
{x ? ? : x ? 2}c)
{x ? ? : x = 2}d)
{x ? ? : -2< x ?2}e)
{x ? ? : x< -2 ou x >2}Resolvi assim:
2x+4 ? 02x+4 =02x=-4 x=-2x-2 < 0x-2 = 0x=2
x=-2x-2 < 0x-2 = 0x=2
Estudo dos snais:
 S={x ? ? : -2? x <2}
S={x ? ? : -2? x <2}Mas a resposta do gabarito é letra A, alguém poderia me explicar como chegar neste resultado?
-

SauloRJ
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 06, 2014 11:08
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por SauloRJ » Qua Jun 04, 2014 13:47
por SauloRJ » Qua Jun 04, 2014 13:47
SauloRJ escreveu:Boa Tarde amigos do fórum!
Estou com dúvida na seguinte questão:
(UF.GO) O conjunto-solução da inequação
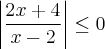
é:
a)
{x ? ? : x = -2}b)
{x ? ? : x ? 2}c)
{x ? ? : x = 2}d)
{x ? ? : -2< x ?2}e)
{x ? ? : x< -2 ou x >2}Resolvi assim:
2x+4 ? 02x+4 =02x=-4 x=-2x-2 < 0x-2 = 0x=2
x=-2x-2 < 0x-2 = 0x=2
Estudo dos snais:
 S={x ? ? : -2? x <2}
S={x ? ? : -2? x <2}Mas a resposta do gabarito é letra A, alguém poderia me explicar como chegar neste resultado?
Poxa, ninguém...
-

SauloRJ
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 06, 2014 11:08
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qua Jun 04, 2014 15:25
por e8group » Qua Jun 04, 2014 15:25
Dica:
Módulo de qualquer número real é não negativo ,isto é , para qualquer número real

tem-se

.
Pois bem , admita que

= conjunto dos números reais

para o qual a desigualdade fornecida por você é verdadeira . Suponha

não vazio . Da suposição , existe

em

tal que
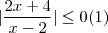
.
Note que
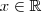
, então
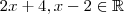
e portanto
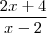
também é um número real o que nos garanti que
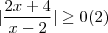
.
Combinando (1) e (2) ,resulta
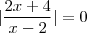
.
Consegue avançar ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por SauloRJ » Qua Jun 04, 2014 19:52
por SauloRJ » Qua Jun 04, 2014 19:52
santhiago escreveu:Dica:
Módulo de qualquer número real é não negativo ,isto é , para qualquer número real

tem-se

.
Pois bem , admita que

= conjunto dos números reais

para o qual a desigualdade fornecida por você é verdadeira . Suponha

não vazio . Da suposição , existe

em

tal que
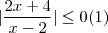
.
Note que
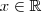
, então
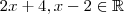
e portanto
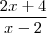
também é um número real o que nos garanti que
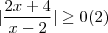
.
Combinando (1) e (2) ,resulta
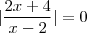
.
Consegue avançar ?
Continuo encontrando x=-2 e x=2, realmente não sei como chegar na resposta do gabarito que é x=-2!
-

SauloRJ
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 06, 2014 11:08
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qua Jun 04, 2014 20:05
por e8group » Qua Jun 04, 2014 20:05
Note que
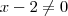
(Caso contrário teríamos indeterminação ) .
Segue ,
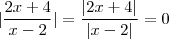
o que implica que
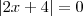
o que implica que
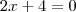
...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7396 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- inequação modular
por manuoliveira » Dom Ago 22, 2010 22:30
- 1 Respostas
- 3481 Exibições
- Última mensagem por Dan

Seg Ago 23, 2010 15:38
Álgebra Elementar
-
- Inequação modular
por scggomes » Qui Abr 21, 2011 17:22
- 3 Respostas
- 3219 Exibições
- Última mensagem por MarceloFantini

Qui Abr 21, 2011 20:54
Cálculo: Limites, Derivadas e Integrais
-
- Inequação Modular
por Rafael16 » Qui Mar 08, 2012 20:24
- 2 Respostas
- 2419 Exibições
- Última mensagem por Rafael16

Qui Mar 08, 2012 21:21
Funções
-
- inequação modular
por haiashi » Qua Jun 06, 2012 00:33
- 0 Respostas
- 1550 Exibições
- Última mensagem por haiashi

Qua Jun 06, 2012 00:33
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
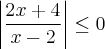 é:
é:




 tem-se
tem-se  .
.  = conjunto dos números reais
= conjunto dos números reais 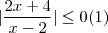 .
. 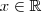 , então
, então 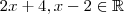 e portanto
e portanto 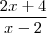 também é um número real o que nos garanti que
também é um número real o que nos garanti que 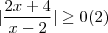 .
.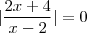 .
.
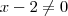 (Caso contrário teríamos indeterminação ) .
(Caso contrário teríamos indeterminação ) . 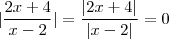 o que implica que
o que implica que 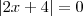 o que implica que
o que implica que 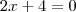 ...
... em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.