a)quanto tempo durou a viagem?
b)Qual foi a velocidade média nos primeiros 100km?
Eu fiz da seguinte maneira:100/(x+40)+100/x=200/96,calculei mmc dos denominadores,mas no fim da conta deu números muito altos e me perdi completamente!!!!


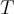 deve ser tal que
deve ser tal que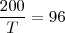 .
.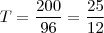 h.
h.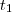 h para percorrer os 100 primeiros kilometros numa velocidade média
h para percorrer os 100 primeiros kilometros numa velocidade média 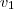 e
e 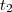 h pra percorrer os outros 100 km numa velocidade média
h pra percorrer os outros 100 km numa velocidade média  , então
, então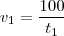 (i)
(i)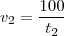 (ii)
(ii)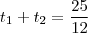 e que (iv)
e que (iv)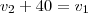 .
.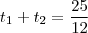
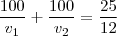
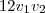 vem que
vem que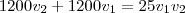 .
.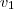 teremos a equação acima transformada em uma equação somente em
teremos a equação acima transformada em uma equação somente em  . Veja:
. Veja: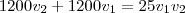
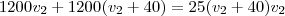
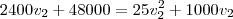
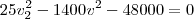
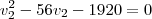
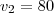 ou
ou 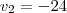 . Já que tratamos a velocidade média como sendo positiva, a 1° solução é a que usaremos.
. Já que tratamos a velocidade média como sendo positiva, a 1° solução é a que usaremos. 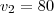 km/h então
km/h então 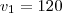 km/h.
km/h.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.