 por phfrito » Qui Mai 08, 2014 19:26
por phfrito » Qui Mai 08, 2014 19:26
Minha dúvida esta no angulo de resolução de 2 problemas.
1º
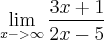
Eu resolvi substituindo o limite primeiramente, ficou:

que diante de meus conhecimentos (corriga se eu estiver errado) é igual a

. No entanto o gabarito simplifca a equação deixando o X em evidencia resultando em

. Se eu estiver correto, porque simplificar a equação?
2º Nao consegui resolver a raiz de limite
![\lim_{x->\infty} \sqrt[]{x} \lim_{x->\infty} \sqrt[]{x}](/latexrender/pictures/b51b152a21547dcc545f8994b6e3b589.png)
Tudo que eu sei sobre as operações básicas entre limites é que podemos multiplicar, dividir, somar e subtrair limites somente com jogo de sinais, a unica inderterminação seria
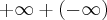
e
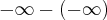
.
alguma objeção?
obrigado pela atenção! ph
-
phfrito
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mai 07, 2014 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por Russman » Qui Mai 08, 2014 23:02
por Russman » Qui Mai 08, 2014 23:02
No 1° caso você obtém por substituição direta de

por

uma indeterminação do tipo

. Ou seja, o limite da função, certamente, é um número. Porém, você não conseguirá calculá-lo da forma que está fazendo. Então, nessas situações, a saída é simplifica a função de modo a obtermos esse número indeterminado a princípio. De fato, se você divide o numerador e denominador por

vai obter tanto no primeiro quanto no último uma parcela do tipo

que, no limite
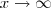
, resulta em

e se obtém a resposta do limite com as parcelas restantes.
No 2° caso quando você substitui

por

obtém, de imediato,

. Este, por sua vez, não é uma indeterminação. Assim, este deve ser o resultado do limite.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por phfrito » Sex Mai 09, 2014 14:26
por phfrito » Sex Mai 09, 2014 14:26
Vi um video na internet que infinito divido por infinito ( se ambos forem positivos) o resultado é infinito?!
-
phfrito
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Mai 07, 2014 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por e8group » Sex Mai 09, 2014 14:36
por e8group » Sex Mai 09, 2014 14:36
Falso . Basta tomar um contra-exemplo ,
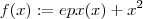
e
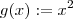
. É claro que
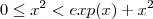
.Logo para qualquer que seja

, tem-se
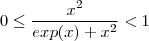
. E além disso , o limite de ambas funções no infnito é

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sex Mai 09, 2014 14:54
por Russman » Sex Mai 09, 2014 14:54
phfrito escreveu:Vi um video na internet que infinito divido por infinito ( se ambos forem positivos) o resultado é infinito?!
Depende da situação. A função
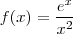
, por exemplo. Se tomarmos o limite
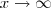
vamos obter, de imediato,

. Como é uma indeterminação precisamos investigar melhor esse limite. Fazendo isso constatamos que, na verdade, essa função tende a

. Quando é indeterminação tudo pode acontecer! kkk Mas, os casos mais famosos são pra limites para números reais como no exemplo do santhiago!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 7563 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3535 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4786 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- Limites no infinito
por felipe_ad » Sáb Abr 24, 2010 15:00
- 3 Respostas
- 5548 Exibições
- Última mensagem por MarceloFantini

Dom Abr 25, 2010 02:27
Cálculo: Limites, Derivadas e Integrais
-
- Limites no infinito
por jr_freitas » Sex Out 07, 2011 16:55
- 10 Respostas
- 10082 Exibições
- Última mensagem por Claudin

Sáb Out 08, 2011 20:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
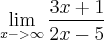
 que diante de meus conhecimentos (corriga se eu estiver errado) é igual a
que diante de meus conhecimentos (corriga se eu estiver errado) é igual a  . No entanto o gabarito simplifca a equação deixando o X em evidencia resultando em
. No entanto o gabarito simplifca a equação deixando o X em evidencia resultando em  . Se eu estiver correto, porque simplificar a equação?
. Se eu estiver correto, porque simplificar a equação?![\lim_{x->\infty} \sqrt[]{x} \lim_{x->\infty} \sqrt[]{x}](/latexrender/pictures/b51b152a21547dcc545f8994b6e3b589.png)
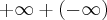 e
e 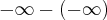 .
. 

 por
por uma indeterminação do tipo
uma indeterminação do tipo  que, no limite
que, no limite 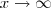 , resulta em
, resulta em  e se obtém a resposta do limite com as parcelas restantes.
e se obtém a resposta do limite com as parcelas restantes.
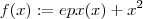 e
e 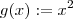 . É claro que
. É claro que 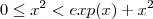 .Logo para qualquer que seja
.Logo para qualquer que seja 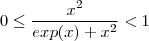 . E além disso , o limite de ambas funções no infnito é
. E além disso , o limite de ambas funções no infnito é 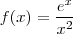 , por exemplo. Se tomarmos o limite
, por exemplo. Se tomarmos o limite