 por leticiapires52 » Qua Abr 16, 2014 10:17
por leticiapires52 » Qua Abr 16, 2014 10:17
Em uma divisão onde o divisor é 4, ache os possíveis restos.
-
leticiapires52
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qua Fev 12, 2014 10:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Qua Abr 16, 2014 11:29
por e8group » Qua Abr 16, 2014 11:29
Dica :
Escreva
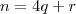
, onde

é o resto .
Primeira possibilidade

, neste caso

divide

.
Segunda possibilidade
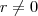
, neste caso

não divide

.
Ora,

não é múltiplo de

. Portanto , n é impar ou par
não múltiplo de

como por exemplo ,
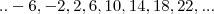
. Observe que esta sequência , pode ser escrita como
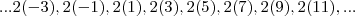
, e vemos que
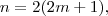
ou
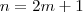
com m inteiro , ou ainda escrevemos
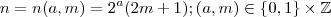
. Assim , definido

, temos
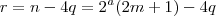
. Podemos escrever
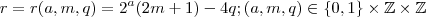
.
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



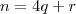 , onde
, onde  é o resto .
é o resto .  , neste caso
, neste caso  divide
divide  .
. 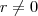 , neste caso
, neste caso  não divide
não divide  .
.  não é múltiplo de
não é múltiplo de  . Portanto , n é impar ou par não múltiplo de
. Portanto , n é impar ou par não múltiplo de  como por exemplo ,
como por exemplo , 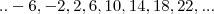 . Observe que esta sequência , pode ser escrita como
. Observe que esta sequência , pode ser escrita como 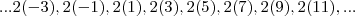 , e vemos que
, e vemos que 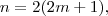 ou
ou 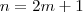 com m inteiro , ou ainda escrevemos
com m inteiro , ou ainda escrevemos 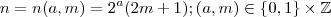 . Assim , definido
. Assim , definido  , temos
, temos 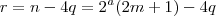 . Podemos escrever
. Podemos escrever 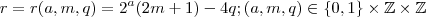 .
. 
