O MDC de um conjuntos de números

é um número

que representa a intersecção entre a fatoração em números primos de cada número
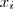
.
Por exemplo,

.
O número
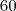
é gerado pelos primos
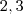
e
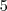
, de modo que

. O

é gerado pelos mesmos, porém na forma

. O

é gerado por um primo a mais:

. Note que

,

e
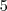
são primos comuns na fatoração de todos os números do conjunto. Assim, você poderá dizer que o MÁXIMO número que é DIVISOR de todos eles, isto é, COMUM, é o número

.
Logicamente,

é divisor comum do conjunto,

é divisor comum do conjuntos,... etc. Mas o maior possível é o produto de todos os primos simultâneos na fatoração dos números do conjunto.
Faz sentido dizer que um conjunto de números

cujo MDC é 1 só possui números primos entre si? Pense.
OBS: Isto não significa que cada número do conjunto é primo! Note que

e nem

nem

são primos. Eles são primos ENTRE SI.


 é um número
é um número  que representa a intersecção entre a fatoração em números primos de cada número
que representa a intersecção entre a fatoração em números primos de cada número 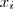 .
. .
.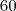 é gerado pelos primos
é gerado pelos primos 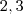 e
e 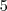 , de modo que
, de modo que  . O
. O  é gerado pelos mesmos, porém na forma
é gerado pelos mesmos, porém na forma  . O
. O  é gerado por um primo a mais:
é gerado por um primo a mais:  . Note que
. Note que  ,
,  e
e  .
. é divisor comum do conjuntos,... etc. Mas o maior possível é o produto de todos os primos simultâneos na fatoração dos números do conjunto.
é divisor comum do conjuntos,... etc. Mas o maior possível é o produto de todos os primos simultâneos na fatoração dos números do conjunto.  e nem
e nem  nem
nem  são primos. Eles são primos ENTRE SI.
são primos. Eles são primos ENTRE SI.