 por kellykcl » Seg Mar 17, 2014 20:42
por kellykcl » Seg Mar 17, 2014 20:42
Boa noite amigos do fórum!
1.Resolva a seguinte inequação:
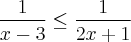
Resolução:
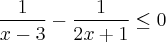
Tirando o m.m.c dos denominadores:
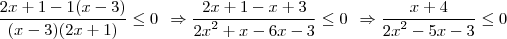
Achando as Raízes:
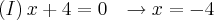
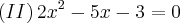

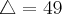
>>>Bhaskara:
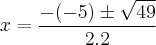
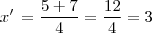
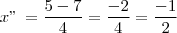
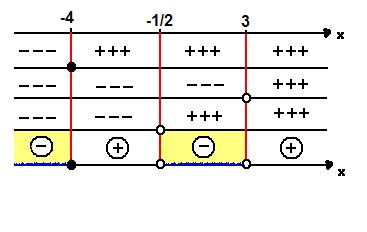
- Estudo dos sinais
- quadro de sinais.JPG (12.64 KiB) Exibido 2424 vezes
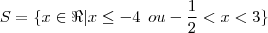
Gostaria que algum amigo mais safo em matemática, verificasse se minha resolução está correta (principalmente o estudo de sinais)!
obs.: Não tenho o gabarito!
Desde já agradeço a colaboração!
"Quem ensina aprende ao ensinar e quem aprende ensina ao aprender."
(Paulo Freire)
-
kellykcl
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Fev 15, 2013 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
 por Russman » Seg Mar 17, 2014 21:24
por Russman » Seg Mar 17, 2014 21:24
Eu acho que você tenha feito um esforço tremendo pra algo simples.
Note que
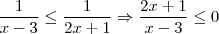
.
Como sabido, a divisão de dois reais só será negativa se os mesmos tiverem sinais trocados. Assim, temos as possibilidades
(1)
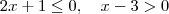
( aqui,

não pode ser

)
(2)
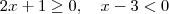
Daí, depois de resolver, retire o caso de

pois é raiz do denominador da equação original como

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por ant_dii » Seg Mar 17, 2014 22:45
por ant_dii » Seg Mar 17, 2014 22:45
Bom, cuidado com a equivalência Russman. Tome
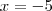
e verifique se vale a relação que você afirmou.
Na verdade ela poderia ter evitado somente o uso de Bháskara, uma vez que

e
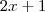
já declaram os valores em que

se anula. Mas fez tudo correto.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por Russman » Seg Mar 17, 2014 22:53
por Russman » Seg Mar 17, 2014 22:53
ant_dii escreveu:Bom, cuidado com a equivalência Russman. Tome e verifique se vale a relação que você afirmou.
Era pra ser "
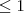
" na inequação! hahah Falta de atenção.
Desconsiderem aí.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por kellykcl » Ter Mar 18, 2014 10:11
por kellykcl » Ter Mar 18, 2014 10:11
Russman escreveu:Eu acho que você tenha feito um esforço tremendo pra algo simples.
Note que
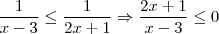
.
Como sabido, a divisão de dois reais só será negativa se os mesmos tiverem sinais trocados. Assim, temos as possibilidades
(1)
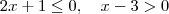
( aqui,

não pode ser

)
(2)
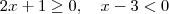
Daí, depois de resolver, retire o caso de

pois é raiz do denominador da equação original como

.
Russman, você multiplicou em Cruz a inequação
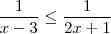
?
"Quem ensina aprende ao ensinar e quem aprende ensina ao aprender."
(Paulo Freire)
-
kellykcl
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Fev 15, 2013 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequações - funções
por lilianers » Sex Mar 29, 2013 21:01
- 1 Respostas
- 973 Exibições
- Última mensagem por e8group

Sáb Mar 30, 2013 13:55
Funções
-
- Inequações
por Bruno 888 » Qua Set 24, 2008 20:36
- 1 Respostas
- 4219 Exibições
- Última mensagem por admin

Ter Set 30, 2008 17:09
Inequações
-
- Inequações
por Rose » Seg Nov 24, 2008 22:44
- 2 Respostas
- 3697 Exibições
- Última mensagem por Rose

Qua Nov 26, 2008 08:18
Inequações
-
- Inequações
 por cristina » Seg Set 07, 2009 01:46
por cristina » Seg Set 07, 2009 01:46
- 2 Respostas
- 2935 Exibições
- Última mensagem por cristina

Seg Set 07, 2009 20:55
Sistemas de Equações
-
- inequações
por jose henrique » Ter Out 26, 2010 23:56
- 10 Respostas
- 6850 Exibições
- Última mensagem por MarceloFantini

Qui Nov 04, 2010 10:31
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
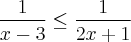
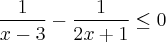
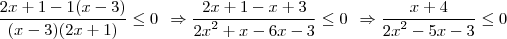
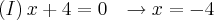
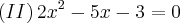

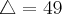
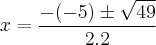
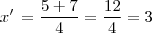
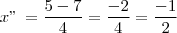
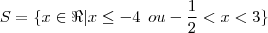


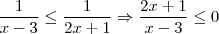 .
.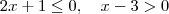 ( aqui,
( aqui,  não pode ser
não pode ser  )
)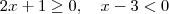
 pois é raiz do denominador da equação original como
pois é raiz do denominador da equação original como  .
.
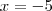 e verifique se vale a relação que você afirmou.
e verifique se vale a relação que você afirmou. e
e 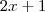 já declaram os valores em que
já declaram os valores em que 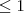 " na inequação! hahah Falta de atenção.
" na inequação! hahah Falta de atenção.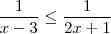 ?
? .
. e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
