 por Edgard Guarido » Sex Mar 07, 2014 18:53
por Edgard Guarido » Sex Mar 07, 2014 18:53
6-(MED. JUNDIAI) Sejam as funções f e g , de R em R, definidas por
f(x) = 2x - 1 e g(x) = kx + t. A função g será inversa de f se, e somente se,
a)k - t = 1
b)k = 2t
c) k + t = 0
d) k = t = ½
não entende por que deu a alternativa d
sendo inversa f(x) e g(x)
f(x)= 2x -1
x/2 +1/2= y
g(x) = kx + t
x/k - t/k = y
por que o resultado da alternativa d
10-(ANGLO) Seja f(x) = 3x e f -¹ a sua inversa. A raiz da equação f(x) = f -¹(x)
é :
a)0
b) 3
c) 1/3
calculando:
f -¹ = x/3
f(X) =f-¹(x) = 3x = x/3 na alternativa da letra A, não sei como desenvolver para dar 0.
quem souber por favor me ajude. E até onde eu fiz está certo?
-
Edgard Guarido
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 07, 2014 17:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia elétrica
- Andamento: cursando
 por Russman » Sáb Mar 08, 2014 19:06
por Russman » Sáb Mar 08, 2014 19:06
Na 1° é só comparar
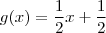
com
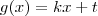
. Daí,
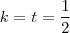
.
Na 2° você obteve uma equação de 1° grau
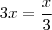
. Resolvendo,
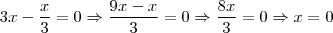
(Pense: que número tem seu triplo igual a sua terça parte? Só pode ser o 0. )
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Edgard Guarido » Qui Mar 13, 2014 15:54
por Edgard Guarido » Qui Mar 13, 2014 15:54
muito obrigado
-
Edgard Guarido
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 07, 2014 17:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [funções inversas]
por Ana_Rodrigues » Ter Jan 24, 2012 17:46
- 2 Respostas
- 1741 Exibições
- Última mensagem por Ana_Rodrigues

Ter Jan 24, 2012 22:33
Funções
-
- Funções circulares inversas
por Ananda » Qui Mar 20, 2008 20:03
- 2 Respostas
- 4810 Exibições
- Última mensagem por Ananda

Seg Mar 24, 2008 17:13
Trigonometria
-
- funçoes circulares inversas
por Thassya » Sex Mai 29, 2009 11:29
- 3 Respostas
- 2531 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 10:18
Trigonometria
-
- Funções Tirgonométricas Inversas
por geriane » Seg Jul 05, 2010 12:06
- 1 Respostas
- 1211 Exibições
- Última mensagem por Tom

Seg Jul 05, 2010 13:07
Trigonometria
-
- trigonometria-funçoes inversas
por henrique_mat » Seg Ago 23, 2010 18:57
- 4 Respostas
- 2615 Exibições
- Última mensagem por henrique_mat

Ter Ago 24, 2010 20:59
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


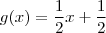 com
com 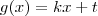 . Daí,
. Daí, 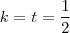 .
.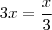 . Resolvendo,
. Resolvendo,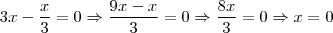

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
