Seja o número complexo Z=a+bi, em que a e b são números reais, a>b,i a unidade imaginária e o seu conjugado. Representando-se geometricamente, no plano de Argand-Gauss, os números Z,-Z, conjugado de Z e o negativo do conjugado de Z, teremos os vértices de um quadrilátero com área e perímetro iguais a 24 unidades de área e 20 unidades de comprimento, respectivamente. É correto afirmar que a forma algébrica de Z é: a)1+5i b)6+4i c)2+3i d)5+i e)3+2i f)I.R.
Bem, eu entendi que perímetro é a soma dos lados, então: Z +(-Z)+(conjugado de Z)+(negativo do conjugado de Z)=20
Então: (a+bi)+(-a-bi)+(a-bi)+(-a+bi)=20 mas ficaria 0=20.. travei aqui. Se puderem me ajudar agradeço. Desculpa nao ter desenvolvido mais..
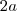e altura 
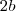, então teremos o seguintes sistem: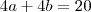
.
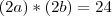
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)