 por fff » Qua Fev 05, 2014 11:54
por fff » Qua Fev 05, 2014 11:54
Bom dia, tenho dúvidas neste exercício que é para resolver com o Teorema de Bolzano:
Sejam f e g duas funções contínuas com domínio [a,b]. Sabe-se que f(a)<g(a) e f(b)>g(b). Prova, por via analítica que os gráficos de f e g se intersetam.
-

fff
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sáb Dez 21, 2013 11:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Informática
- Andamento: cursando
 por e8group » Qua Fev 05, 2014 15:26
por e8group » Qua Fev 05, 2014 15:26
Dica :
Defina
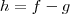
. Mostre que

é contínua e que
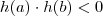
e com isso conclua que existe
![c \in [a,b] c \in [a,b]](/latexrender/pictures/89a48a2849559c11ee668929aa8a973f.png)
de modo que
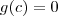
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fff » Qua Fev 05, 2014 16:57
por fff » Qua Fev 05, 2014 16:57
Eu fiz assim:
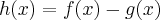
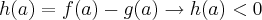
porque
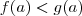
.
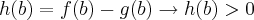
porque
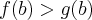
.
Como h é contínua (pois é a diferença de 2 funções contínuas) e
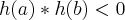
, o corolário do Teorema de Bolzano permite afirmar que :
Existe
![x\epsilon]a,b[:h(x)=0 x\epsilon]a,b[:h(x)=0](/latexrender/pictures/1512fd5253a447b726d0dfbf8a5497c6.png)
. Então o gráfico de f e g intersetam-se.
-

fff
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sáb Dez 21, 2013 11:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Informática
- Andamento: cursando
 por e8group » Qui Fev 06, 2014 11:17
por e8group » Qui Fev 06, 2014 11:17
Está correto sua solução .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de bolzano
por Fabricio dalla » Qua Mar 07, 2012 12:54
- 1 Respostas
- 1479 Exibições
- Última mensagem por MarceloFantini

Qua Mar 07, 2012 19:16
Funções
-
- Método da Bissecção Teorema de Bolzano
por romulo39 » Qua Out 12, 2011 00:05
- 1 Respostas
- 1847 Exibições
- Última mensagem por LuizAquino

Qua Out 12, 2011 09:14
Cálculo: Limites, Derivadas e Integrais
-
- Teorema de Pitágoras, exercício
 por LuizCarlos » Sáb Mai 05, 2012 17:30
por LuizCarlos » Sáb Mai 05, 2012 17:30
- 3 Respostas
- 1820 Exibições
- Última mensagem por sony01

Sáb Mai 05, 2012 21:33
Trigonometria
-
- Teorema das linhas
por valleska » Seg Mai 18, 2009 21:46
- 1 Respostas
- 3268 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 11:20
Desafios Enviados
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4686 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



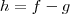 . Mostre que
. Mostre que  é contínua e que
é contínua e que 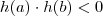 e com isso conclua que existe
e com isso conclua que existe ![c \in [a,b] c \in [a,b]](/latexrender/pictures/89a48a2849559c11ee668929aa8a973f.png) de modo que
de modo que 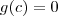 .
.
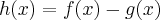
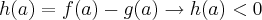 porque
porque 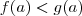 .
.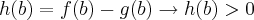 porque
porque 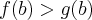 .
.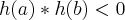 , o corolário do Teorema de Bolzano permite afirmar que :
, o corolário do Teorema de Bolzano permite afirmar que :![x\epsilon]a,b[:h(x)=0 x\epsilon]a,b[:h(x)=0](/latexrender/pictures/1512fd5253a447b726d0dfbf8a5497c6.png) . Então o gráfico de f e g intersetam-se.
. Então o gráfico de f e g intersetam-se.


