 por marysuniga » Qua Jan 29, 2014 14:36
por marysuniga » Qua Jan 29, 2014 14:36
-
marysuniga
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Dez 19, 2013 15:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
 por e8group » Qua Jan 29, 2014 16:46
por e8group » Qua Jan 29, 2014 16:46
Boa tarde p/ todos ...
Substituição simples (também) resolve o problema . Seja
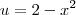
Logo ,
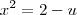
e

. Assim ,
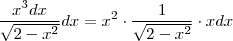
. Daí ,substituindo-se
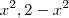
e
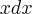
pelas expressões correspondentes (em termos de u) respectivamente , obteremos
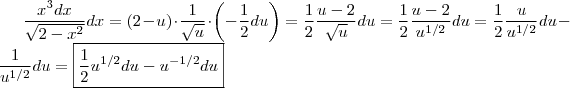
.
Integrando a expressão destacada e voltando para variável original terá a resposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marysuniga » Sex Jan 31, 2014 14:09
por marysuniga » Sex Jan 31, 2014 14:09
Obrigada

-
marysuniga
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Dez 19, 2013 15:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Biomédica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida
por gdarius » Ter Mar 16, 2010 15:57
- 5 Respostas
- 5639 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:32
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2715 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3993 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5057 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 2
por DanielFerreira » Sáb Mar 31, 2012 18:31
- 1 Respostas
- 2074 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{{x}^{3}dx}{\sqrt[2]{2 - {x}^{2}}} \int_{}^{}\frac{{x}^{3}dx}{\sqrt[2]{2 - {x}^{2}}}](/latexrender/pictures/67f164ed00de0db3402ad60cf790dc4b.png)
![\sqrt[2]{2}sent \sqrt[2]{2}sent](/latexrender/pictures/625bf482cd1d1e8d3c1049f91d8a0639.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-{\left(\sqrt[]{2}sent \right)}^{2}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-{\left(\sqrt[]{2}sent \right)}^{2}}} \sqrt[]{2}cost dt](/latexrender/pictures/abc744d2e467a06e1818408809e0976a.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2{sen}^{2}t}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2{sen}^{2}t}}} \sqrt[]{2}cost dt](/latexrender/pictures/7df5983f9d9efcdf4312257524098efb.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2\left (1 -{cos}^{2}t)}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2\left (1 -{cos}^{2}t)}}} \sqrt[]{2}cost dt](/latexrender/pictures/a2bca28309e161aea915f2339e2f4436.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2{cos}^{2}t}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2{cos}^{2}t}}} \sqrt[]{2}cost dt](/latexrender/pictures/e830ece9e8ac66209cb2f3181acc4b92.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2}cost}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2}cost}} \sqrt[]{2}cost dt](/latexrender/pictures/98add89ba1fb66a2a73d7466816bec1d.png)
![\int_{}^{} 2\sqrt[]{2}{sen}^{3}t dt \int_{}^{} 2\sqrt[]{2}{sen}^{3}t dt](/latexrender/pictures/ddc8a5ebdffc1c288229f9b058c208cf.png)
![2\sqrt[]{2}\int_{}^{}{sen}^{3}t 2\sqrt[]{2}\int_{}^{}{sen}^{3}t](/latexrender/pictures/91b6d7e7cc84608d2e7a9bcb303250be.png)

![\int_{}^{}\frac{{x}^{3}dx}{\sqrt[2]{2 - {x}^{2}}} \int_{}^{}\frac{{x}^{3}dx}{\sqrt[2]{2 - {x}^{2}}}](/latexrender/pictures/67f164ed00de0db3402ad60cf790dc4b.png)
![\sqrt[2]{2}sent \sqrt[2]{2}sent](/latexrender/pictures/625bf482cd1d1e8d3c1049f91d8a0639.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-{\left(\sqrt[]{2}sent \right)}^{2}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-{\left(\sqrt[]{2}sent \right)}^{2}}} \sqrt[]{2}cost dt](/latexrender/pictures/abc744d2e467a06e1818408809e0976a.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2{sen}^{2}t}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2{sen}^{2}t}}} \sqrt[]{2}cost dt](/latexrender/pictures/7df5983f9d9efcdf4312257524098efb.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2\left (1 -{cos}^{2}t)}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2-2\left (1 -{cos}^{2}t)}}} \sqrt[]{2}cost dt](/latexrender/pictures/a2bca28309e161aea915f2339e2f4436.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2{cos}^{2}t}}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2{cos}^{2}t}}} \sqrt[]{2}cost dt](/latexrender/pictures/e830ece9e8ac66209cb2f3181acc4b92.png)
![\int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2}cost}} \sqrt[]{2}cost dt \int_{}^{}\frac{{\left(\sqrt[]{2}sent)}^{3}}{\sqrt[]{2}cost}} \sqrt[]{2}cost dt](/latexrender/pictures/98add89ba1fb66a2a73d7466816bec1d.png)
![\int_{}^{} 2\sqrt[]{2}{sen}^{3}t dt \int_{}^{} 2\sqrt[]{2}{sen}^{3}t dt](/latexrender/pictures/ddc8a5ebdffc1c288229f9b058c208cf.png)
![2\sqrt[]{2}\int_{}^{}{sen}^{3}t 2\sqrt[]{2}\int_{}^{}{sen}^{3}t](/latexrender/pictures/91b6d7e7cc84608d2e7a9bcb303250be.png)

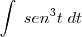
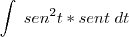
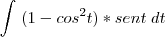
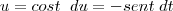 .
.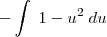


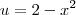 Logo ,
Logo , 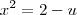 e
e  . Assim ,
. Assim , 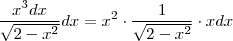 . Daí ,substituindo-se
. Daí ,substituindo-se 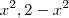 e
e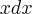 pelas expressões correspondentes (em termos de u) respectivamente , obteremos
pelas expressões correspondentes (em termos de u) respectivamente , obteremos 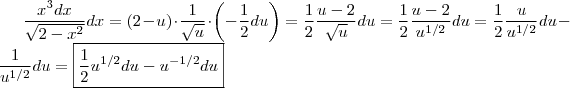 .
.


