A soma dos coeficientes do desenvolvimento de
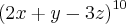 é necessariamente:
é necessariamente:a) um número maior que
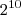
b) um número entre
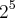 e
e 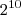
c) igual a 1
d) igual a zero
e) um número negativo.

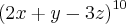 é necessariamente:
é necessariamente: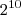
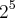 e
e 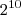

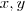 .Esta soma a uma potência
.Esta soma a uma potência 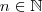 se escreve como
se escreve como 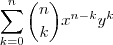 (Teorema Binomial ) e igualdade
(Teorema Binomial ) e igualdade 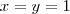 nos dá a soma dos coeficientes acima
nos dá a soma dos coeficientes acima 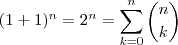 . E quando temos
. E quando temos  números reais
números reais 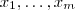 ,o teorema multinomial nos garanti uma forma de expandir
,o teorema multinomial nos garanti uma forma de expandir 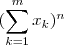 como se vê lá ...
como se vê lá ... 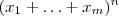 na sua forma expandida . Fazendo todos
na sua forma expandida . Fazendo todos 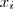 iguais a
iguais a  , teremos
, teremos 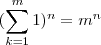 que és a soma requerida .
que és a soma requerida .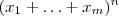 se escreve sob a soma das parcelas que se exprimem por
se escreve sob a soma das parcelas que se exprimem por 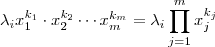 ;
; 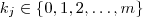 ,esta afirmação é assegurada pelo teorema multinomial , ou então notando a fórmula de recorrência :
,esta afirmação é assegurada pelo teorema multinomial , ou então notando a fórmula de recorrência : 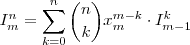 .Em que a notação
.Em que a notação 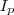 designa a soma dos primeiros
designa a soma dos primeiros  termos da lista
termos da lista 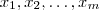 ,i.e.,
,i.e., 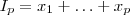 .
.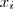 iguais
iguais  teremos a soma dos coeficientes
teremos a soma dos coeficientes 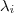 .
.
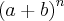 é dada por
é dada por 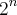 (isso é bem observado no triângulo de Pascal, certo?). Mas o teorema multinomial eu não compreendi. Procurei alguma informação na internet, mas não consegui entender.
(isso é bem observado no triângulo de Pascal, certo?). Mas o teorema multinomial eu não compreendi. Procurei alguma informação na internet, mas não consegui entender.
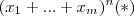 pelo teorema multinomial .Mas isto não importa ,só queremos a soma dos coeficiente de
pelo teorema multinomial .Mas isto não importa ,só queremos a soma dos coeficiente de  na sua forma expandida .
na sua forma expandida . 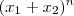 e
e 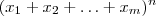 nas suas formas expandida . Segue ,
nas suas formas expandida . Segue , 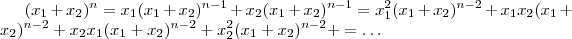
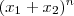 se exprima como
se exprima como 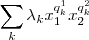 com
com 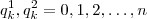 e
e 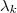 números reais . Quando fizemos
números reais . Quando fizemos 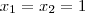 teremos a soma dos coeficientes
teremos a soma dos coeficientes 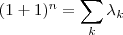 .
.silviopuc escreveu: teorema binomial eu entendi. Sei que a soma dos coeficientes de um binômio é dada por (isso é bem observado no triângulo de Pascal, certo?)
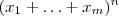 se escreva como
se escreva como 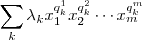 (
(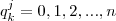 ) e novamente se fizermos
) e novamente se fizermos 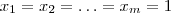 teremos a soma dos coeficientes que és
teremos a soma dos coeficientes que és  . No se exercício tente identificar o termo geral da soma . Tente concluir .
. No se exercício tente identificar o termo geral da soma . Tente concluir .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: