 por Gustavo Gomes » Ter Dez 10, 2013 22:15
por Gustavo Gomes » Ter Dez 10, 2013 22:15
Olá, pessoal!
Seja r a raiz positiva da equação

.
Qual é o valor de
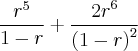
?
A resposta é 1.
Não consegui resolver... Algumas resoluções que pesquisei utilizam a igualdade:
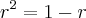
. Não entendi como a raiz r satisfaz essa equação...
Aguardo. Grato.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por e8group » Qua Dez 11, 2013 17:36
por e8group » Qua Dez 11, 2013 17:36
Gustavo Gomes escreveu:Olá, pessoal!
Seja r a raiz positiva da equação

.
Qual é o valor de
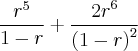
?
A resposta é 1.
Não consegui resolver... Algumas resoluções que pesquisei utilizam a igualdade:
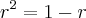
. Não entendi como a raiz r satisfaz essa equação...
Aguardo. Grato.
Note que por hipótese ,
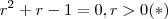
e assim ,
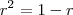
.
Em relação ao exercício , só manipular tal expressão e utilizar (*) .
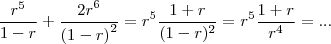
. Avance .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação do segundo grau] Relação entre raíz e coeficiente
por Gustavo Gomes » Sex Fev 14, 2014 21:44
- 1 Respostas
- 1609 Exibições
- Última mensagem por DanielFerreira

Seg Fev 17, 2014 15:06
Equações
-
- (UNICAMP) Raíz real positiva
por Carolziiinhaaah » Sex Fev 04, 2011 15:32
- 0 Respostas
- 1219 Exibições
- Última mensagem por Carolziiinhaaah

Sex Fev 04, 2011 15:32
Álgebra Elementar
-
- Equação do segundo grau
por VtinxD » Qui Jan 27, 2011 23:03
- 1 Respostas
- 3903 Exibições
- Última mensagem por douglaspezzin

Dom Jun 19, 2011 09:55
Desafios Médios
-
- Equação de segundo grau
por maria cleide » Seg Mai 09, 2011 23:46
- 3 Respostas
- 2695 Exibições
- Última mensagem por FilipeCaceres

Ter Mai 10, 2011 00:43
Sistemas de Equações
-
- Equação do segundo grau
por LuizCarlos » Qui Mai 10, 2012 13:01
- 3 Respostas
- 3116 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 12, 2012 20:41
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.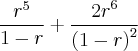 ?
?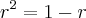 . Não entendi como a raiz r satisfaz essa equação...
. Não entendi como a raiz r satisfaz essa equação...
 .
.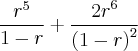 ?
?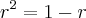 . Não entendi como a raiz r satisfaz essa equação...
. Não entendi como a raiz r satisfaz essa equação...
.
?
. Não entendi como a raiz r satisfaz essa equação...
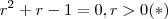 e assim ,
e assim , 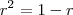 .
.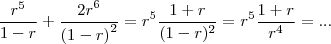 . Avance .
. Avance .