calcular a área da funçao

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

calcular a área da funçao

Regras do fórum
Responder

calcular a área da funçao

Mensagempor edilaine33 » Dom Dez 01, 2013 08:54

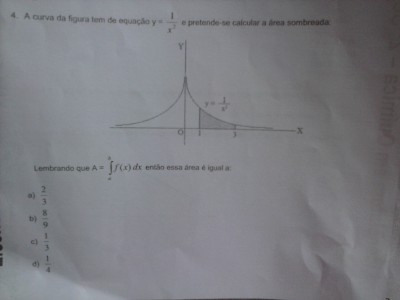
calcular a área da função calculo integral.
Anexos
P29-11-13_14.35.jpg
edilaine33
Novo Usuário
Novo Usuário
 
Mensagens: 7
Registrado em: Sáb Nov 30, 2013 14:14
Formação Escolar: GRADUAÇÃO
Área/Curso: licenciatura em quimica
Andamento: cursando
Voltar ao topo

Re: calcular a área da funçao

Mensagempor Pessoa Estranha » Dom Dez 01, 2013 10:13

Olá !

\int_{1}^{3}\frac{1}{{x}^{2}}dx

Encontrar a primitiva:

\int_{}^{}\frac{1}{{x}^{2}}dx = -{x}^{-1} + k

Fazer: primitiva avaliada de [1,3];

\int_{1}^{3}\frac{1}{{x}^{2}} = - ({3)}^{-1} - [-({1)}^{-1}] = -\frac{1}{3} + 1 = \frac{-1 + 3}{3} = \frac{2}{3}.

Certo?

Como você tentou fazer?
Pessoa Estranha
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 262
Registrado em: Ter Jul 16, 2013 16:43
Formação Escolar: GRADUAÇÃO
Área/Curso: Matemática
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 


Tópico Popular

Assunto: [Função] do primeiro grau e quadratica
Autor: Thassya - Sáb Out 01, 2011 16:20

1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?

2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?

3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?

Assunto: [Função] do primeiro grau e quadratica
Autor: Neperiano - Sáb Out 01, 2011 19:46

Ola

Qual as suas dúvidas?

O que você não está conseguindo fazer?

Nos mostre para podermos ajudar

Atenciosamente

Assunto: [Função] do primeiro grau e quadratica
Autor: joaofonseca - Sáb Out 01, 2011 20:15

1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.

y_{b}-y_{a}=m(x_{b}-x_{a})

1-3=m(-3-1) \Leftrightarrow -2=-4m \Leftrightarrow m=\frac{2}{4} \Leftrightarrow m=\frac{1}{2}

Em y=mx+b substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.

3=\frac{1}{2} \cdot 1+b\Leftrightarrow 3-\frac{1}{2}=b \Leftrightarrow b=\frac{5}{2}



2)Na equação y=x^2-5x+9 não existem zeros.Senão vejamos

Completando o quadrado,

(x^2-5x+\frac{25}{4})+9-\frac{25}{4} =0\Leftrightarrow (x-\frac{5}{2})^2+\frac{11}{4}=0

As coordenadas do vertice da parabola são (\frac{5}{2},\frac{11}{4})

O eixo de simetria é a reta x=\frac{5}{2}.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.

f(-7)=93
f(10)=59

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum