É o seguinte: "Determine os polinômios
 do terceiro grau tais que
do terceiro grau tais que 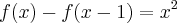 ."
."Minha resolução:
Seja
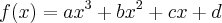 . Conforme a informação fornecida, temos:
. Conforme a informação fornecida, temos: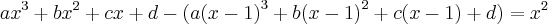
Então, desenvolvendo tudo, obtemos:
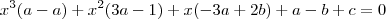
Daí, como precisamos encontrar os valores dos coeficientes,
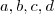 , então basta resolver o sistema, resultando em:
, então basta resolver o sistema, resultando em: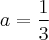
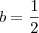
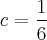
É neste ponto que estou com dúvida. Ocorre que o coeficiente
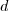 não apareceu no sistema. É claro que o coeficiente
não apareceu no sistema. É claro que o coeficiente 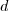 é uma constante, mas a questão é: como seria a resposta ? Apenas:
é uma constante, mas a questão é: como seria a resposta ? Apenas: 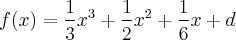 ?
?Achei um tanto estranho e , então, gostaria de uma opinião.




 , avisa que eu resolvo.
, avisa que eu resolvo.

