que contem um capacitor com capacitância de C Farads (F); um resistor
com uma resistência de R ohms (
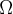 ); com carga Q medida em coulombs; voltagem E(t)
); com carga Q medida em coulombs; voltagem E(t) medida em volts e o tempo t medido em segundos.
Supondo que , R=2
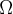 , C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i
, C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i no instante t. (observação a corrente i é dada por i = dQ/dt ).
Me ajudem por favor é urgente preciso enviar a prova até dia 27/08 terça feira.



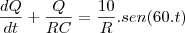














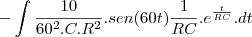






 .
.
 :
: