É um exercício que pede para usar a regra de L´Hospital.
Pensei que pudesse ser um caso de função limitada e então, o resultado seria o limite do sen(x), mas fiquei insegura com relação a isto. Contudo, ao tentar usar a regra de L´Hospital, tentei transformar a "expressão" num quociente e então, aplicar a regra; mas não ajudou em nada.
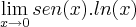
(x tende a zero pela direita).


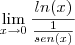
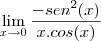
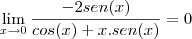

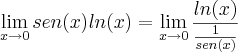
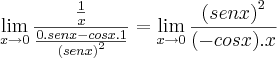
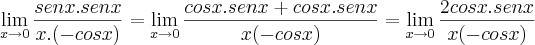
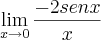
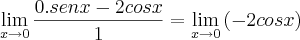
 .
. 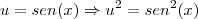
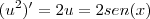
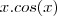 , que tb precisa ser derivado (regra do produto):
, que tb precisa ser derivado (regra do produto):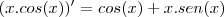
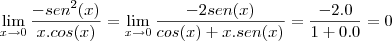

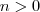 de modo que
de modo que 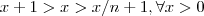 . Como a função
. Como a função 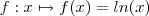 é injetora (ela é estritamente crescente) então
é injetora (ela é estritamente crescente) então 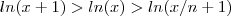 e portanto
e portanto 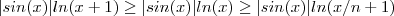 ocorrendo a igualdade somente quando
ocorrendo a igualdade somente quando 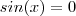 para
para  . Como
. Como 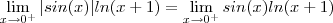 e além disso ,
e além disso , 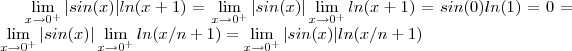 .
.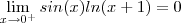 .
.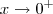 pois
pois 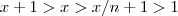 .Por favor desconsiderem .
.Por favor desconsiderem .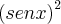 por uma variável
por uma variável  ; contudo, não posso aplicar a regra do produto?
; contudo, não posso aplicar a regra do produto?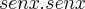
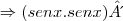 =
= 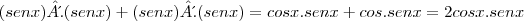 .
.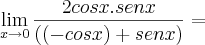
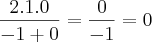 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)