 por zenildo » Qui Ago 22, 2013 15:31
por zenildo » Qui Ago 22, 2013 15:31
Qual a razão da P.A.( 2,-10,...). Determine o 6° termo dessa progressão.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Renato_RJ » Qui Ago 22, 2013 15:50
por Renato_RJ » Qui Ago 22, 2013 15:50
Boa tarde !!!
Veja, você tem o 1º e o 2º termo, a razão de uma P.A. será a diferença entre esses termos pois

, em posse dessa informação (a razão) use:
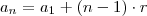
Para obter o 6º termo (

).
Espero ter ajudado !!
Qualquer coisa, posta aí...
Abraços...
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por zenildo » Qui Ago 22, 2013 16:44
por zenildo » Qui Ago 22, 2013 16:44
eu tentei fazer assim;
A6= 2+( 6-1).-12
A6= -58
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Luis Gustavo » Qui Ago 22, 2013 17:06
por Luis Gustavo » Qui Ago 22, 2013 17:06
A
razão é a diferença entre um termo e seu anterior em uma P.A.
Para achar a razão, que é representada pela letra

, é só pegar qualquer termo da P.A. e subtrair dele o termo anterior.
Para achar o

termo, é só você ir somando a razão que achou até completar seis termos, ou então usar a fórmula do termo geral da P.A.





Já ensinei a fazer, agora, se quer a resposta pronta, não posso te ajudar.
Espero ter ajudado.
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6139 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4729 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5633 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4428 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8403 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , em posse dessa informação (a razão) use:
, em posse dessa informação (a razão) use: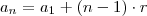
 ).
).

 , é só pegar qualquer termo da P.A. e subtrair dele o termo anterior.
, é só pegar qualquer termo da P.A. e subtrair dele o termo anterior. termo, é só você ir somando a razão que achou até completar seis termos, ou então usar a fórmula do termo geral da P.A.
termo, é só você ir somando a razão que achou até completar seis termos, ou então usar a fórmula do termo geral da P.A.




