Olá Zenildo!
Sugiro que dê uma lida no tópico sobre como utilizar o
para escrever expressões matemáticas.
A equação é
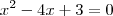
.
Encontre as raízes por Bháskara.
Acredito que possamos supor, neste exercício, que ou a sequência é uma progressão geométrica ou aritmética.
Como tens dois termos sucessivos da sequência (as raízes

e

), ache a razão

para os dois casos.
Se a sequência for geométrica, a razão será

. Se for aritmética, a razão será

.
Depois, verifique para qual dessas duas opções (geométrica ou aritmética) o terceiro termo da sequência é igual a
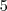
. Acredito que somente uma das duas opções terá o terceiro termo igual a
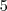
.
Descobrindo se a sequência é uma progressão geométrica ou aritmética, fica fácil calcular qualquer termo dela.
Qualquer dúvida, comente.
Abraço!



 para escrever expressões matemáticas.
para escrever expressões matemáticas.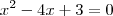 .
. e
e  ), ache a razão
), ache a razão  para os dois casos.
para os dois casos. . Se for aritmética, a razão será
. Se for aritmética, a razão será  .
.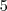 . Acredito que somente uma das duas opções terá o terceiro termo igual a
. Acredito que somente uma das duas opções terá o terceiro termo igual a 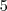 .
.

 .
.
 :
: