 por zenildo » Dom Ago 04, 2013 16:08
por zenildo » Dom Ago 04, 2013 16:08
OS NÚMEROS X,3X-2 E 2X+5 SÃO RESPECTIVAMENTE O SEXTO, O SÉTIMO E O OITAVO TERMOS DE UMA P.A. O CENTESIMO PRIMEIRO TERMO DA P.A.É IGUAL A:
A) 380
B) 381
C) 382
D) 383
E) 384
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por DanielFerreira » Dom Ago 04, 2013 21:03
por DanielFerreira » Dom Ago 04, 2013 21:03
De acordo com o enunciado,

,

e

.
Temos que

, e também

.
Igualando a razão, já que são iguais, temos:

Sendo

, logo,

;
Encontremos
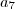
substituindo x pelo valor encontrado acima.

Obtendo a razão r:

Para finalizar,
 Alternativa d
Alternativa d.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ,
,  e
e  .
. , e também
, e também  .
.
 , logo,
, logo,  ;
;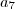 substituindo x pelo valor encontrado acima.
substituindo x pelo valor encontrado acima.





 , avisa que eu resolvo.
, avisa que eu resolvo.

