 por fabriel » Dom Jun 23, 2013 01:32
por fabriel » Dom Jun 23, 2013 01:32
E ai pessoal, estou na duvida nesse exercicio... Vejam:
Se w=f(x,y), em que
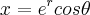
e

, mostre que,
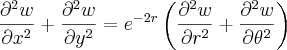
Resolvendo.... Sei que..
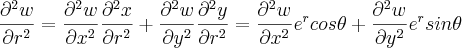
e
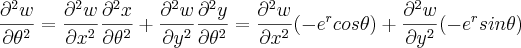
E quando vou somar a expressão
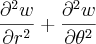
vai zera:
Onde eu errei nos calculos?
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Dom Jun 23, 2013 11:54
por young_jedi » Dom Jun 23, 2013 11:54
Na verdade você tem que

calculando a derivada segunda teremos que

para teta é a mesma coisa, comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por fabriel » Dom Jun 23, 2013 13:50
por fabriel » Dom Jun 23, 2013 13:50
hummm obrigado aiestou começando a compreender essa passagem.
Mas a minha duvida é em relação a essa expressão por exemplo:
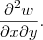
Como ficaria essa expressão?
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Seg Jun 24, 2013 18:52
por young_jedi » Seg Jun 24, 2013 18:52
como não sabemos qual é a relação de w com x e y, não tem como calcular essa parcela
mais repare que esta parcela aparece duas vezes na expressão, o esperado é que ao substituir os valores das demais derivadas parciais e fazendo a soma com a derivada parcial com relação a teta você consiga cancelar essas duas parcela.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- FUNÇÃO DE DUAS VARIÁVEIS; DERIVADAS
por anselmojr97 » Seg Nov 09, 2015 02:14
- 4 Respostas
- 3764 Exibições
- Última mensagem por anselmojr97

Ter Nov 10, 2015 00:02
Cálculo: Limites, Derivadas e Integrais
-
- Problema com duas variáveis
por helen_chaves » Qua Jun 03, 2009 12:00
- 3 Respostas
- 4131 Exibições
- Última mensagem por Cleyson007

Sex Jun 05, 2009 12:51
Funções
-
- Limite de duas variaveis
por Tixa11 » Seg Abr 01, 2013 13:13
- 1 Respostas
- 2199 Exibições
- Última mensagem por young_jedi

Qua Abr 03, 2013 11:09
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Duas variaveis
por fabriel » Sáb Jun 15, 2013 16:48
- 2 Respostas
- 2491 Exibições
- Última mensagem por temujin

Sáb Jun 15, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Função de duas variáveis
por lilianers » Qua Ago 21, 2013 19:37
- 1 Respostas
- 2368 Exibições
- Última mensagem por Renato_RJ

Qui Ago 22, 2013 12:46
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
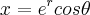 e
e  , mostre que,
, mostre que,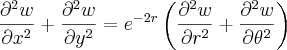
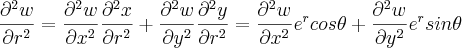
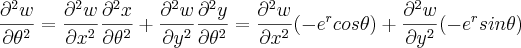
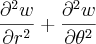 vai zera:
vai zera:
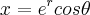 e
e  , mostre que,
, mostre que,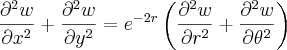
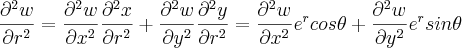
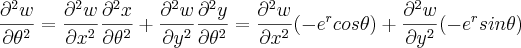
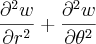 vai zera:
vai zera:



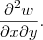



 .
.
 :
: