 por Lenin » Sex Mai 31, 2013 03:10
por Lenin » Sex Mai 31, 2013 03:10
Pessoal, estou com dificuldades em resolver essa função:
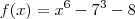
o resultado dela é 2 e -1.. eu consigo responder quando é elevado a quarta tipo essa:
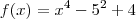
que os zeros são 2, -1, 1 e -2..trocando o
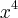
por outra incógnita tipo
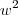
..mas com

não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por e8group » Sex Mai 31, 2013 14:43
por e8group » Sex Mai 31, 2013 14:43
Por favor ,confirma se as funções são
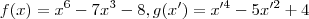
.Caso sejam ,podemos fazer
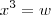
e
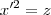
(Por quê ?) Assim ,
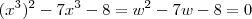
e
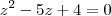
.
Ambas expressões podem ser calculadas pela fórmula resolvente .Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lenin » Sex Mai 31, 2013 23:49
por Lenin » Sex Mai 31, 2013 23:49
santhiago escreveu:Por favor ,confirma se as funções são
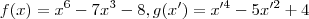
.Caso sejam ,podemos fazer
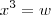
e
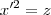
(Por quê ?) Assim ,
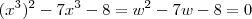
e
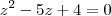
.
Ambas expressões podem ser calculadas pela fórmula resolvente .Tente concluir .
não entendi muito..
É tipo assim brother: eu fiz assim:
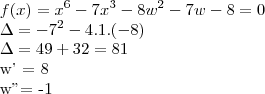
a partir dai não sei o que fazer.. como a resposta é x = 2 e 1, eu presumo que pego o w = 8 e faço
![{x}^{3} = 8
x = \sqrt[3]{8} = 2 {x}^{3} = 8
x = \sqrt[3]{8} = 2](/latexrender/pictures/b30ff66eecb340ed6150a37453d30c43.png)
só que como o w" = -1, não ha raiz real, só imaginária, ou
![x = \sqrt[3]{-1} = 1 x = \sqrt[3]{-1} = 1](/latexrender/pictures/6c37998a534d7ac1ebce45e28aa97d5a.png)
? há alguma regra para índice ímpar com radicando -1 seja igual a 1?
só vejo assim para o que eu achei coincide com o gabarito .
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por e8group » Sáb Jun 01, 2013 12:30
por e8group » Sáb Jun 01, 2013 12:30
Note que
![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png)
,pois ,
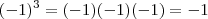
.Além disso ,
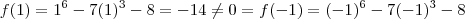
.Comente as dúvidas .
Observação :
Quando o índice

é impar e o radicando

é negativo ,o número é
![\sqrt[n]{a} < 0 \sqrt[n]{a} < 0](/latexrender/pictures/261ff9994999d43972a2ad6e6aa7238e.png)
é real ,casso fosse

par ,
![\sqrt[n]{a} \notin \mathbb{R} \sqrt[n]{a} \notin \mathbb{R}](/latexrender/pictures/94826bbc3ed30a99672afbb1ec6cfacd.png)
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Zeros da funcao
por sergiosilva » Qua Jan 05, 2011 22:59
- 3 Respostas
- 3875 Exibições
- Última mensagem por MarceloFantini

Qui Jan 06, 2011 21:13
Funções
-
- determinar os zeros da função
por anamendes » Dom Abr 29, 2012 12:37
- 1 Respostas
- 5822 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 14:06
Trigonometria
-
- Determinar os zeros da sequinte função
por franciscokael » Qui Out 21, 2010 15:36
- 2 Respostas
- 1917 Exibições
- Última mensagem por Elcioschin

Qui Out 28, 2010 17:07
Funções
-
- Dada uma função, calcular os zeros
por Tixa11 » Sáb Nov 10, 2012 12:26
- 4 Respostas
- 2958 Exibições
- Última mensagem por Tixa11

Seg Nov 12, 2012 18:05
Funções
-
- Descobrir zeros
por Tixa11 » Qui Jan 24, 2013 19:17
- 2 Respostas
- 1658 Exibições
- Última mensagem por Tixa11

Sex Jan 25, 2013 20:30
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
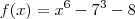
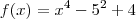
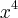 por outra incógnita tipo
por outra incógnita tipo 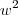 ..mas com
..mas com  não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.
não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.

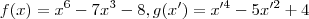 .Caso sejam ,podemos fazer
.Caso sejam ,podemos fazer 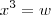 e
e 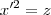 (Por quê ?) Assim ,
(Por quê ?) Assim , 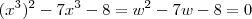 e
e 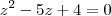 .
.
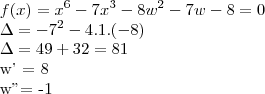
![{x}^{3} = 8
x = \sqrt[3]{8} = 2 {x}^{3} = 8
x = \sqrt[3]{8} = 2](/latexrender/pictures/b30ff66eecb340ed6150a37453d30c43.png)
![x = \sqrt[3]{-1} = 1 x = \sqrt[3]{-1} = 1](/latexrender/pictures/6c37998a534d7ac1ebce45e28aa97d5a.png) ? há alguma regra para índice ímpar com radicando -1 seja igual a 1?
? há alguma regra para índice ímpar com radicando -1 seja igual a 1?![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png) ,pois ,
,pois , 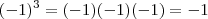 .Além disso ,
.Além disso , 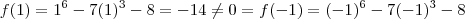 .Comente as dúvidas .
.Comente as dúvidas . é impar e o radicando
é impar e o radicando  é negativo ,o número é
é negativo ,o número é ![\sqrt[n]{a} < 0 \sqrt[n]{a} < 0](/latexrender/pictures/261ff9994999d43972a2ad6e6aa7238e.png) é real ,casso fosse
é real ,casso fosse ![\sqrt[n]{a} \notin \mathbb{R} \sqrt[n]{a} \notin \mathbb{R}](/latexrender/pictures/94826bbc3ed30a99672afbb1ec6cfacd.png) .
.




