 por arnoanderson » Qui Nov 05, 2009 22:00
por arnoanderson » Qui Nov 05, 2009 22:00
Minha segunda dúvida à respeito de derivadas, porém acredito que esteja com dificuldade é na fatoração:
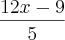
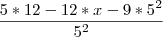
Não consigo desenvolver a partir dali. O resultado é
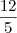
mas não consigo chegar nesse valor.
Obrigado
-
arnoanderson
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 01, 2009 16:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Lucio Carvalho » Sex Nov 06, 2009 08:54
por Lucio Carvalho » Sex Nov 06, 2009 08:54
Olá arnoanderson,
Para derivares a função

podes pensar da seguinte maneira:

Logo,


Espero ter ajudado e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por arnoanderson » Sex Nov 06, 2009 12:15
por arnoanderson » Sex Nov 06, 2009 12:15
Obrigado pela ajuda, Lucio.
E certamente, até breve!
-
arnoanderson
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Nov 01, 2009 16:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada
por alienpuke » Sáb Out 24, 2015 15:45
- 2 Respostas
- 6988 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2015 16:12
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda em Derivada
por vinim » Qua Jun 02, 2010 21:20
- 1 Respostas
- 1336 Exibições
- Última mensagem por MarceloFantini

Qui Jun 03, 2010 03:46
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda Derivada.
por jhonniewalk » Qui Mai 24, 2012 16:49
- 5 Respostas
- 2632 Exibições
- Última mensagem por DanielFerreira

Qui Mai 31, 2012 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda
por Bruna Cintra » Ter Mai 29, 2012 10:44
- 1 Respostas
- 1210 Exibições
- Última mensagem por Jhonata

Ter Mai 29, 2012 11:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
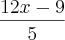
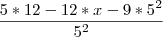
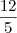 mas não consigo chegar nesse valor.
mas não consigo chegar nesse valor.
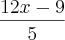
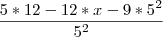
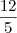 mas não consigo chegar nesse valor.
mas não consigo chegar nesse valor.
 podes pensar da seguinte maneira:
podes pensar da seguinte maneira:









