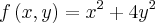 Usando as curvas de nivel de altuta = k 0,1,2,3,4,5.
Usando as curvas de nivel de altuta = k 0,1,2,3,4,5.não consugo faze esse exercicio, por favor mi de uma mão.

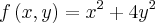 Usando as curvas de nivel de altuta = k 0,1,2,3,4,5.
Usando as curvas de nivel de altuta = k 0,1,2,3,4,5.
Silva339 escreveu:Esboce o mapa de contornos deUsando as curvas de nivel de altuta = k 0,1,2,3,4,5.
não consugo faze esse exercicio, por favor mi de uma mão.

marinalcd escreveu:Silva339 escreveu:Esboce o mapa de contornos deUsando as curvas de nivel de altuta = k 0,1,2,3,4,5.
não consugo faze esse exercicio, por favor mi de uma mão.
Bom, esse exercício é bem simples, tendo só que desenhar as curvas de nível.
Para montar o gráfico aqui fica difícil, mas é só você fazer no mesmo gráfico as curvas:
x² + 4y² = 0
x² + 4y² = 1
x² + 4y² = 2
x² + 4y² = 3
x² + 4y² = 4
x² + 4y² = 5
São curvas bem simples de desenhar, e costumamos trabalhar bastante no dia-a-dia com elas.
Tente fazer e se ajudar, faça o esboço dessas curvas, no winplot, por exemplo, assim, você pode confirmar sua resposta.



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: