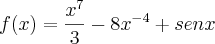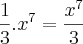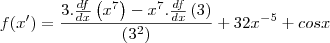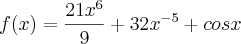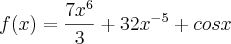por jeferson lopes » Qui Mai 02, 2013 13:58
por jeferson lopes » Qui Mai 02, 2013 13:58
Puts, esse professor de cálculo quer acabar comigo!! estava indo tudo muito bem quando derrepente!!
f(x)=1/3*x^7 -8x^-4+sen x (1 sobre 3, vezes x elevado a 7, menos 8x elevado a menos 4 + seno de x). Complicou tudo!!! por favor me ajudem, esse exercício vale ponto.
-
jeferson lopes
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Mar 25, 2013 10:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Sobreira » Qui Mai 02, 2013 15:27
por Sobreira » Qui Mai 02, 2013 15:27
Amigo você já tentou utilizar o LaTeX para editar suas expresões??
Assim ficaria mais fácil para tentar ajudá-lo.
A função a que você se referiu é esta?
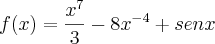
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por jeferson lopes » Qui Mai 02, 2013 15:44
por jeferson lopes » Qui Mai 02, 2013 15:44
Boa tarde Sobreira! desculpe. Não deu certo.
(um dividido por 3, vezes x elevado a 7. o restante está corretor.
Obrigado!
-
jeferson lopes
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Mar 25, 2013 10:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Sobreira » Qui Mai 02, 2013 16:14
por Sobreira » Qui Mai 02, 2013 16:14
Pois bem:
Neste caso eu já efetuei a multiplicação de
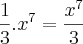
Prosseguindo:
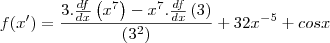
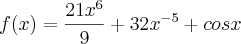
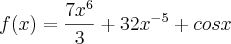
Se não entender alguma parte pode comentar, porque a intenção não é entregar o exercício pronto e sim transmitir o conceito utilizado para que seja possível resolver qualquer problema.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3810 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- fração
por leandro moraes » Qui Jan 14, 2010 19:41
- 1 Respostas
- 1695 Exibições
- Última mensagem por MarceloFantini

Qui Jan 14, 2010 20:09
Estatística
-
- Fração
por bia rosendo » Seg Jun 06, 2011 11:45
- 2 Respostas
- 4518 Exibições
- Última mensagem por Claudin

Seg Jun 06, 2011 18:34
Matemática Financeira
-
- Fração 110
por Raphael Feitas10 » Seg Jan 09, 2012 17:28
- 1 Respostas
- 1851 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 09, 2012 18:43
Sistemas de Equações
-
- Fração 112
por Raphael Feitas10 » Sex Jan 13, 2012 02:23
- 1 Respostas
- 1673 Exibições
- Última mensagem por ant_dii

Sex Jan 13, 2012 03:18
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.