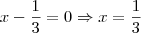the points where the function f(x)= [x] + |1 -x|, -1<=x<=3, where [.] denotes the greatest integer function, is not differentiable, are:
resolução;
![f(x)= \left[x \right]+\left|1 -x \right| f(x)= \left[x \right]+\left|1 -x \right|](/latexrender/pictures/8bdd9ca74d806c44fa118b5c768cc948.png) .......,
......., 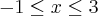
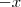 ...................
...................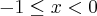
 ...................
...................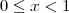
 ...................
...................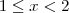
 ...................
...................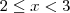
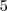 ...................
...................
the only doubtful points are x = -1, 0, 1, 2, and 3. It can be easily seen that f(x) is differentiable at x= -1 but not differentiable at x = 0, 1, 2, and 3.


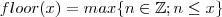 .
. 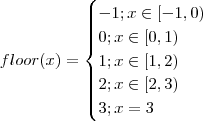 .
. 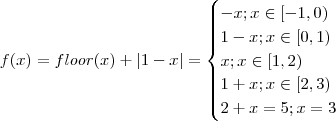 .
.  .Nos pontos em que a função é descontínua,pelo Lemma "Derivabilidade implica continuidade " podemos descartar a possibilidade da diferenciabilidade nestes pontos .Mas cuidado !! O recíproco deste Lemma não é verdadeiro .Nos pontos em que
.Nos pontos em que a função é descontínua,pelo Lemma "Derivabilidade implica continuidade " podemos descartar a possibilidade da diferenciabilidade nestes pontos .Mas cuidado !! O recíproco deste Lemma não é verdadeiro .Nos pontos em que 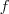 é contínua devemos calular a derivada via definição .
é contínua devemos calular a derivada via definição . 
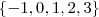 .
.  é contínua em
é contínua em  .
. 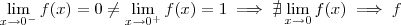 não é contínua em 0 .
não é contínua em 0 . 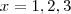 ,o argumento é semelhante .Deixo como exercício p/ tentar concluir .
,o argumento é semelhante .Deixo como exercício p/ tentar concluir . 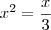
 .
.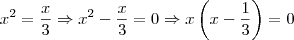
 :
: