 por chronoss » Dom Abr 21, 2013 16:52
por chronoss » Dom Abr 21, 2013 16:52
Sejam a, b ,c números reais positivos distintos dois a dois tais que a² + b² - ab = c² .
Prove que o produto ( a - c )( b - c ) é negativo
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Seg Abr 22, 2013 12:11
por young_jedi » Seg Abr 22, 2013 12:11
da equação nos tiramos que

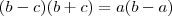
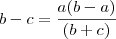
mis tabme podemos ter que

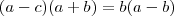
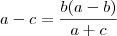
então
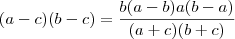
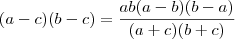
como todos os numero são postivos, então o denominador (a+c)(b+c) tambem é positivo e o produto ab tabem é positivo
mas se b-a for positivo então a-b é negativo
e se b-a for negativo então a-b é positivo
ou seja uma das duas é negtiva, como os demais termos são positivos então o resultado é algo negativo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por e8group » Seg Abr 22, 2013 13:36
por e8group » Seg Abr 22, 2013 13:36
Pensei de outra forma também .
A prova é por contradição (não é única,há outras possibilidades) .
Vamos supor que o produto
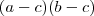
é positivo ,isto é ,
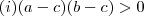
.
O item

ocorrerá
(ii)
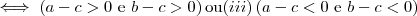
Mas ,foi dado que

.Deixando

em evidência e somando-se
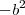
em ambos membros ,obtemos que
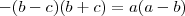
.Como
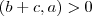
,decorre que (iv)

e
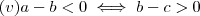
.Além disso ,pela suposição do produto ser positivo ,segue
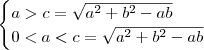
.
Desenvolvendo ambas inequações ,obtemos que
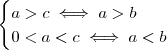
.
Conclusão : O item (ii) contradiz (iv) ,da mesma forma , (iii) conttradiz (v) ,logo o produto
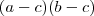
é negativo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por chronoss » Seg Abr 22, 2013 14:23
por chronoss » Seg Abr 22, 2013 14:23
Obrigado aos dois.
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prove: n(A X B) = n(A) * n(B)
por juliomarcos » Dom Set 14, 2008 02:58
- 3 Respostas
- 5288 Exibições
- Última mensagem por admin

Qua Set 24, 2008 05:33
Conjuntos
-
- Prove que
por Balanar » Dom Ago 29, 2010 17:22
- 1 Respostas
- 2318 Exibições
- Última mensagem por MarceloFantini

Seg Ago 30, 2010 01:24
Álgebra Elementar
-
- Prove
por chronoss » Seg Abr 29, 2013 20:40
- 1 Respostas
- 1993 Exibições
- Última mensagem por chronoss

Sáb Mai 04, 2013 13:55
Álgebra Elementar
-
- PROVE
por pedro22132938 » Sex Ago 21, 2015 20:10
- 1 Respostas
- 2836 Exibições
- Última mensagem por e8group

Dom Ago 23, 2015 20:21
Cálculo: Limites, Derivadas e Integrais
-
- Prove que:
por serhumano0100 » Sex Fev 28, 2020 14:44
- 2 Respostas
- 3174 Exibições
- Última mensagem por adauto martins

Sáb Mar 07, 2020 12:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



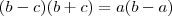
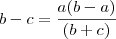

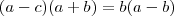
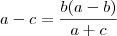
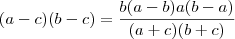
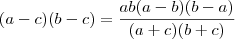

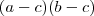 é positivo ,isto é ,
é positivo ,isto é , 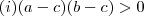 .
.  ocorrerá
ocorrerá 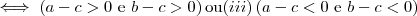
 .Deixando
.Deixando  em evidência e somando-se
em evidência e somando-se 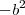 em ambos membros ,obtemos que
em ambos membros ,obtemos que 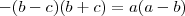 .Como
.Como 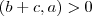 ,decorre que (iv)
,decorre que (iv) e
e 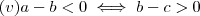 .Além disso ,pela suposição do produto ser positivo ,segue
.Além disso ,pela suposição do produto ser positivo ,segue 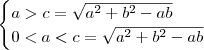 .
. 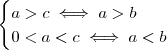 .
.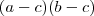 é negativo .
é negativo .