Determine
 para que a equação do segundo grau
para que a equação do segundo grau 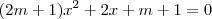 tenha raízes reais tais que
tenha raízes reais tais que 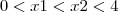
Gabatiro :
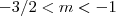

 para que a equação do segundo grau
para que a equação do segundo grau 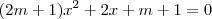 tenha raízes reais tais que
tenha raízes reais tais que 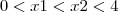
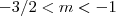

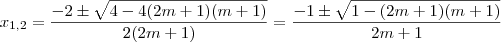 .
.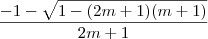
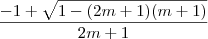 .
.  vemos que obrigatoriamente
vemos que obrigatoriamente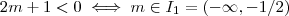 (Por quê ?) .Assim ,como
(Por quê ?) .Assim ,como 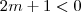 então
então 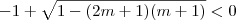 .Desta forma, além de termos que impor que
.Desta forma, além de termos que impor que 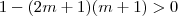 (já que há duas soluções distintas p/ equação) teremos também que tomar
(já que há duas soluções distintas p/ equação) teremos também que tomar 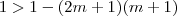 .
.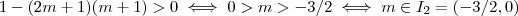 (Por favor ,faça as contas)
(Por favor ,faça as contas)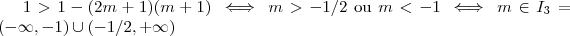
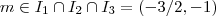 , ou seja ,para qualquer
, ou seja ,para qualquer 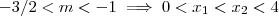 .
.
 e produto
e produto 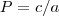 das raízes em que
das raízes em que  e
e 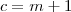 .Pela restrição ,
.Pela restrição , 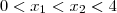 obtemos que ,
obtemos que ,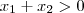
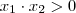
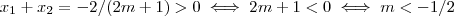 .
.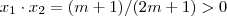 que devido a
que devido a 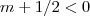 implica
implica 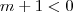 e portanto
e portanto 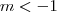 .
.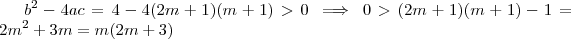 .
.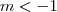 ,o produto
,o produto 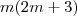 é negativo sse
é negativo sse 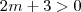 . Desenvolvendo segue o resultado do gabarito .
. Desenvolvendo segue o resultado do gabarito .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

