 por Victor Gabriel » Dom Abr 14, 2013 21:01
por Victor Gabriel » Dom Abr 14, 2013 21:01
Determine o valor da soma: S = 0,2+0,22+0,222+..
Qual é o valor 3S?
assim: S=
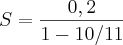
S=2,2
logo S.3= 2,2.3=6,6
Estou certo?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Seg Abr 15, 2013 21:08
por e8group » Seg Abr 15, 2013 21:08
Acredito que está incorreto .
Observe que ,
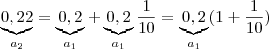
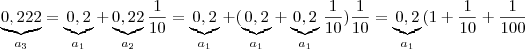
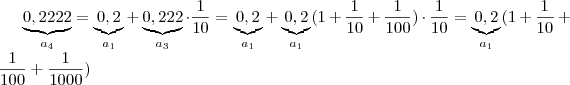
(...)
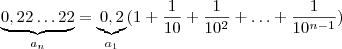
(...)
Imagine a soma destas infinitas parcelas
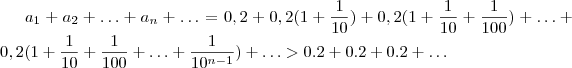
.
Qual a sua estimativa para o valor da soma acima ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2101 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- Soma de PG
por a_guia » Seg Jan 04, 2010 22:19
- 1 Respostas
- 2034 Exibições
- Última mensagem por Molina

Seg Jan 04, 2010 22:54
Progressões
-
- Soma
por manuoliveira » Dom Mai 30, 2010 18:23
- 1 Respostas
- 8389 Exibições
- Última mensagem por Douglasm

Dom Mai 30, 2010 20:08
Binômio de Newton
-
- SOMA DE PA
por cristiano » Seg Mai 16, 2011 16:18
- 1 Respostas
- 1691 Exibições
- Última mensagem por Molina

Seg Mai 16, 2011 20:44
Progressões
-
- SOMA DE UMA PA
por silvia fillet » Qua Fev 15, 2012 19:50
- 1 Respostas
- 1836 Exibições
- Última mensagem por silvia fillet

Sáb Fev 18, 2012 11:24
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




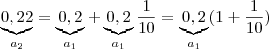
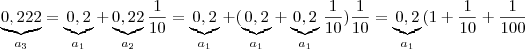
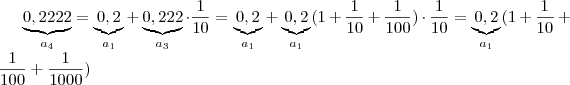
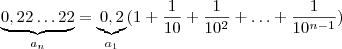
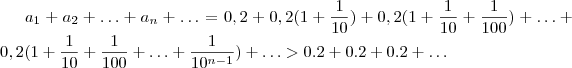 .
.

 .
.
 :
: