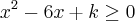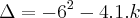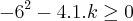por laura_biscaro » Seg Abr 08, 2013 22:44
por laura_biscaro » Seg Abr 08, 2013 22:44
Para que a função real f(x)=
![\sqrt[2]{{x}^{2}-6x+k} \sqrt[2]{{x}^{2}-6x+k}](/latexrender/pictures/31716b1885aade6f30cd4148d988f551.png)
, onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que:
a) k

5
b)k=9
c)k=5
d)k

9
e)k

9
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Seg Abr 08, 2013 23:18
por Russman » Seg Abr 08, 2013 23:18
É só tomar o radicando maior ou igual a zero, pois a raiz quadrada somente se define para números positivos e o zero.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por laura_biscaro » Seg Abr 08, 2013 23:26
por laura_biscaro » Seg Abr 08, 2013 23:26
então, meu resultado só ta sendo k

5, e a resposta é k

9 :s
-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Ter Abr 09, 2013 00:11
por e8group » Ter Abr 09, 2013 00:11
Observe que a expressão que estar dentro do radicando é uma polinômio do segundo grau , sendo assim ,a função

estará bem definida

existirem
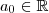
e

tal que a equação

pode ser escrita como (i)

e (ii)

.Desenvolvendo ambas expressões , e por igualdade de polinômios ,temos que :
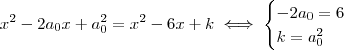
.Neste caso ,

.
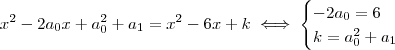
.Neste caso
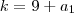
para qualquer
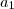
positivo ;logo , obrigatoriamente

para a função

estar bem definida .
Outra forma seria observar que se
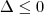
ou seja ,

a função estaria bem definida nesta situação .
Editado alguns erros digitados ....
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por anabatista » Ter Abr 09, 2013 00:31
por anabatista » Ter Abr 09, 2013 00:31
Teriamos que
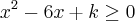
logo
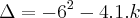
Como esse valor também será incluso na raiz, ele tambem devera ser maior ou igual a zero
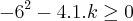
E assim se encontra a resposta
-
anabatista
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Abr 08, 2013 23:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por laura_biscaro » Ter Abr 09, 2013 00:38
por laura_biscaro » Ter Abr 09, 2013 00:38
obrigada pessoal! agora eu consegui chegar na resposta

-
laura_biscaro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Fev 18, 2013 19:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{{x}^{2}-6x+k} \sqrt[2]{{x}^{2}-6x+k}](/latexrender/pictures/31716b1885aade6f30cd4148d988f551.png) , onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que:
, onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que: 5
5 9
9 9
9
![\sqrt[2]{{x}^{2}-6x+k} \sqrt[2]{{x}^{2}-6x+k}](/latexrender/pictures/31716b1885aade6f30cd4148d988f551.png) , onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que:
, onde x e k são reais, seja definida para qualquer valor de x, k deverá ser um número tal que: 5
5 9
9 9
9

 5, e a resposta é k
5, e a resposta é k 9 :s
9 :s
 estará bem definida
estará bem definida  existirem
existirem 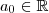 e
e  tal que a equação
tal que a equação  pode ser escrita como (i)
pode ser escrita como (i)  e (ii)
e (ii) .Desenvolvendo ambas expressões , e por igualdade de polinômios ,temos que :
.Desenvolvendo ambas expressões , e por igualdade de polinômios ,temos que : 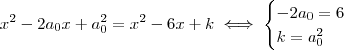 .Neste caso ,
.Neste caso ,  .
. 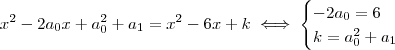 .Neste caso
.Neste caso 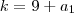 para qualquer
para qualquer 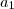 positivo ;logo , obrigatoriamente
positivo ;logo , obrigatoriamente  para a função
para a função estar bem definida .
estar bem definida . 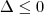 ou seja ,
ou seja ,  a função estaria bem definida nesta situação .
a função estaria bem definida nesta situação .