[Geometria espacial] Centros de simetria

por **rochadapesada** » Seg Abr 08, 2013 21:57

Essa questão não sei nem como começar... Uma luz por favor

Os centros de simetria das faces de um cubo de aresta a são os vértices de um poliedro cujo volume é dado por:

a) ${a}^{3}\sqrt{7}$

b) ${a}^{3}\sqrt{5}$

c) $\frac{{a}^{3}}{12}$

d $)\frac{{a}^{3}\sqrt{3}}{4}$

e) n.d.a

por **young_jedi** » Qua Abr 10, 2013 15:32

o poliedro e a figura em vermelho

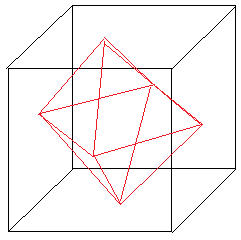
: cubo.png (3.61 KiB) Exibido 1964 vezes

repare que ele se trata de duas piramedes uma invertida da outra então calculando o volume de uma das piramedes encontramos o volume do poliedro sendo o dobro desta

a base das piramedes é um quadrado onde seus vertices estão nos centros das faces portanto, utilizando teorema de pitagoras vemos que o lado deste quadrado é

$x^2=\left(\frac{a}{2}\right)^2+\left(\frac{a}{2}\right)^2$

portanto

$x=a.\frac{\sqrt2}{2}$

portanto a area do quadrado é

$x^2=\frac{a^2}{2}$

a altura da piramede é a/2 tente calcular o volume da piramede e do poliedro e comente as duvidas

por **rochadapesada** » Qua Abr 10, 2013 16:15

Obrigado cara =D

[Geometria espacial] Centros de simetria

[Geometria espacial] Centros de simetria

[Geometria espacial] Centros de simetria

Re: [Geometria espacial] Centros de simetria

Re: [Geometria espacial] Centros de simetria

Quem está online