 por Fabricio dalla » Sex Mar 29, 2013 20:30
por Fabricio dalla » Sex Mar 29, 2013 20:30
![\int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx \int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx](/latexrender/pictures/ffac9ea0931e3ae66b1dbd114c8ab7ed.png)
Não sei como começar
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marinalcd » Sex Mar 29, 2013 21:52
por marinalcd » Sex Mar 29, 2013 21:52
Fabricio dalla escreveu:![\int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx \int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx](/latexrender/pictures/ffac9ea0931e3ae66b1dbd114c8ab7ed.png)
Não sei como começar
Esta integral não é muito complicada nem muito extensa.
Basta você realizar uma substituição simples.
A derivada de arctg 1/x é fácil, né?
Ao fazer a substituição, você pode tratar como uma integral indefinida, assim você não precisa mudar os limites de integração. Aí no final, quando você voltar à variável do problema, você substitui os limites. Ou então, logo após fazer a substituição simples, você muda o intervalo de integração.
Tente fazer!
Qualquer dúvida poste aqui!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Fabricio dalla » Sex Mar 29, 2013 23:08
por Fabricio dalla » Sex Mar 29, 2013 23:08
pois é cara eu começo a desenvolver o problema nem é a integral que vem depois mas sim a parte
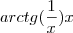
que com o intervalo dado dá arctg(1/0) ai n existe...
eu fiz isso que vc falou na integral
![\int_{0}^{\sqrt[2]{3}}\frac{{x}^{3}}{{x}^{2}+1}
com u={x}^{2}+1 \int_{0}^{\sqrt[2]{3}}\frac{{x}^{3}}{{x}^{2}+1}
com u={x}^{2}+1](/latexrender/pictures/70ee05c7274ca9632f3116e72f092b53.png)
mas n resolve o problema...
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx \int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx](/latexrender/pictures/ffac9ea0931e3ae66b1dbd114c8ab7ed.png)

![\int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx \int_{0}^{\sqrt[2]{3}}arctg(\frac{1}{x})dx](/latexrender/pictures/ffac9ea0931e3ae66b1dbd114c8ab7ed.png)


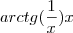 que com o intervalo dado dá arctg(1/0) ai n existe...
que com o intervalo dado dá arctg(1/0) ai n existe...![\int_{0}^{\sqrt[2]{3}}\frac{{x}^{3}}{{x}^{2}+1}
com u={x}^{2}+1 \int_{0}^{\sqrt[2]{3}}\frac{{x}^{3}}{{x}^{2}+1}
com u={x}^{2}+1](/latexrender/pictures/70ee05c7274ca9632f3116e72f092b53.png) mas n resolve o problema...
mas n resolve o problema...





