(puc-sp) Os Termos da sequência (10,8,11,9,12,10,13....) obedecem a uma lei de formação. Se an, em que n
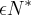 , é o termo de ordem n dessa sequência, então a30+a55 é igual a :
, é o termo de ordem n dessa sequência, então a30+a55 é igual a :
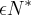 , é o termo de ordem n dessa sequência, então a30+a55 é igual a :
, é o termo de ordem n dessa sequência, então a30+a55 é igual a :
 ,
, 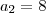 ,...
,...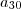 devemos utilizar a 'segunda' sequência, pois ela fornece os termos pares, com isso:
devemos utilizar a 'segunda' sequência, pois ela fornece os termos pares, com isso: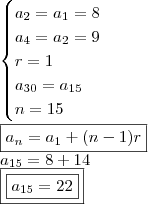
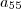 através da 1ª sequência. Mas, há um detalhe!
através da 1ª sequência. Mas, há um detalhe! e depois somar uma unidade, uma vez que a razão é UM!!
e depois somar uma unidade, uma vez que a razão é UM!!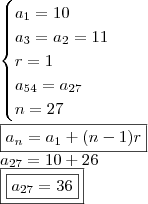
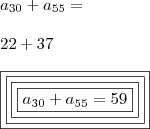

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes